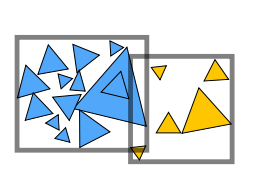
包围盒(Bounding Volumes)
将复杂的物体用简单的包围盒包裹是一个减少无用射线相交计算的好方式
- 物体完整地包含在包围盒里
- 如果射线不与包围盒相交则不与物体相交
- 因而优先检测包围盒是否相交再检测是否与物体相交
射线与包围盒相交(Ray-Intersection With Box)
注意理解:盒子是三对平面的交汇处,这三个平面即为包围盒边界
特别的我们通常使用轴对齐包围盒(Axis-Aligned Bounding Box),简称 AABB
Bounding Box(BB)的任意一侧沿着X,Y,或Z轴
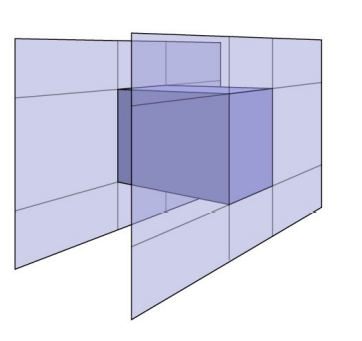
射线与轴对称包围盒相交(Ray Intersection with Axis-Aligned Box)
以下2D例子在3D场景中同样适用
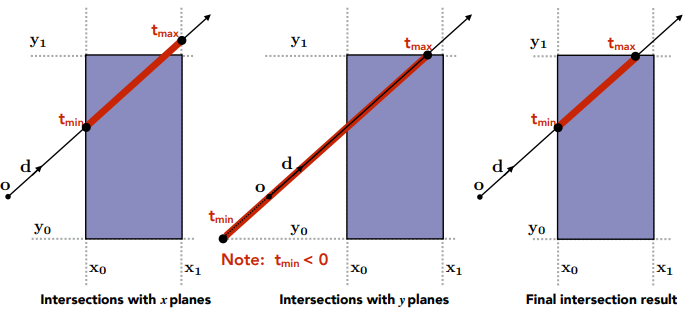
如上图所示,我们分别计算射线与包围盒两个边界的相交时间点,求取到$t_{min}/t_{max}$的交集
- 射线只有同时进入所有对平面才算进入包围盒,离开包围盒同理
- 对于每一对平面,计算$t_{min}和t_{max}$,允许出现负值
对于3D包围盒,$t_{enter} = \max{t_{min}},t_{exit} = \min{t_{max}}$
如果$t_{enter}<t_{exit}$,我们便可得知射线在盒子内停留了一段时间(必定发生了相交)
注意点:
- 光线并非一条线,应当检查是否为负值或是否符合物理
- $t_{exit}<0$的时候,包围盒在射线之外,没有相交
- $t_{exit}>=0和t_{enter}$时,光线的起始点在包围盒内,相交
选择轴对称的原因:计算量少
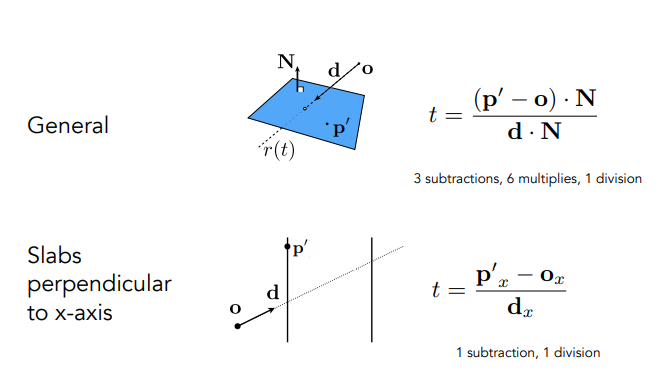
统一空间分区\网格(Uniform Spatial Partitions/Grids)
划分过程
找到包围盒
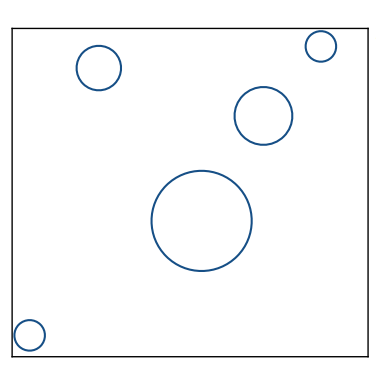
创建网格
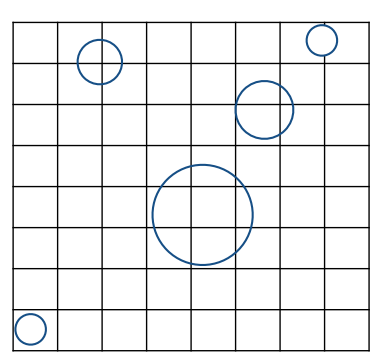
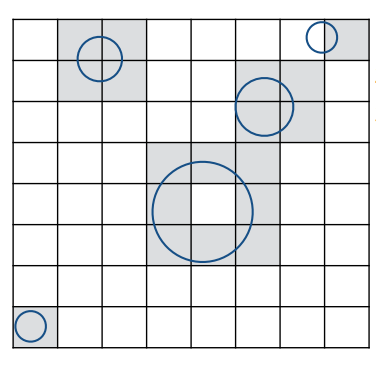
在与相应物体重叠的网格中存储对应的物体
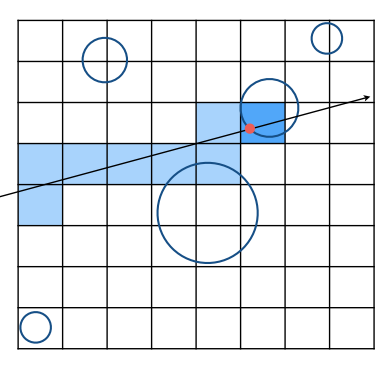
根据射线穿过的网格顺序来遍历网格
对于每一个被遍历的网格,需要检测其中存储的物体是否与射线相交
网格数量
网格仅有一个时无法起到加速算法的效果
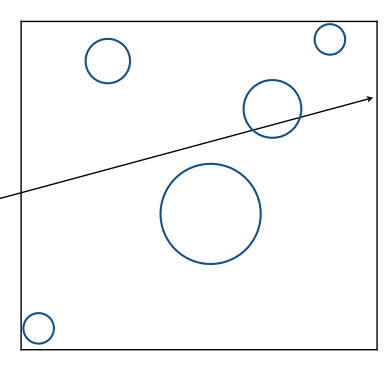
网格过多时,因需要遍历过多无关网格而低效
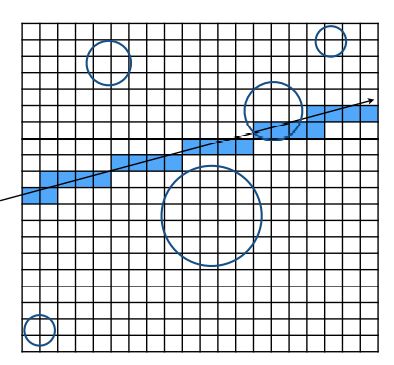
最佳的网格数量为: $$cells = C * objs$$ $$C \approx 27 \ \ in \ \ 3D$$
划分空间网格的方式往往在大小和空间均匀分布的大型对象集合的情况下有良好的效果
在失效的情况下会产生" Teapot in a stadium "问题,即在一个大运动场中间放了一个茶壶,此时需要走很多格子才能找到场景中茶壶的交点,在场景分布不均匀的情况下不适用网格方法
空间划分(Spatial Partitions)
八叉树(Oct-Tree)
将整个场景包围在盒中,再将包围盒切分为8份(三维情况下,每面四块),下图展示的是二维下的情况,将整个盒子分为四块,再将每块都分成四块,直到每个格子中无物体或物体数量足够少
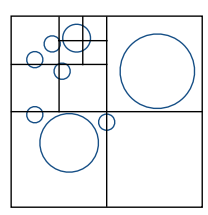
通过这种方式将空间切成了分块并组织成了树状结构(一维下为二叉树,二维下为四叉树,三维下为八叉树,$n维下为2^n叉树$)
BSP-Tree
该方法是对空间进行二分的方法,即每次都选择一个方向将节点划分开,与KD-Tree不同在于其并非横平竖直地划分,且计算难度随维度升高而增加
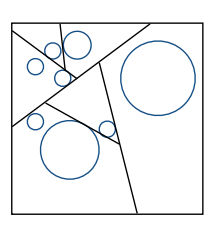
二维下用一条线划分,三维下用一个平面划分,四维用‘超平面’划分,依次类推
KD-Tree
与八叉树几乎相同,但每找到一个格子后总是沿着某一个轴分开使整个空间被划分成类似二叉树的结构,如下图所示,划分是水平竖直交替进行的
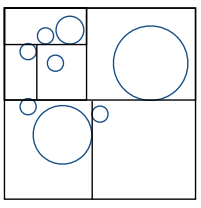
三维下,划分轴在X,Y,Z轴间轮替就可以在保持二叉树性质的情况下进行划分
KD-Tree建立
将整个场景包围在盒子A中,先沿着竖直方向划分,再将这两个部分横向划分开,之后一直交替向下划分,形成一棵树
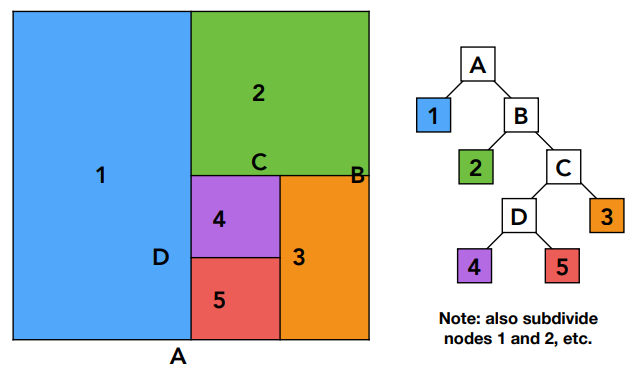
如果一个空间已经被划分成了KD-Tree结构,则中间节点(A,B,C,D)只需要记录被划分成的各自格子,叶子节点则存储和格子相交的几何形体
KD-Tree的数据结构
内部节点存储:
- 划分的轴:X,Y,Z轴
- 划分的点:沿轴的平面分割坐标
- 子内部节点:指向子节点的坐标
- 在根节点不存储物体
叶子节点存储:
- 物体的列表(list of objects)
KD-Tree的遍历
假设有一根光线,从左上到右下,穿过一个包围盒A
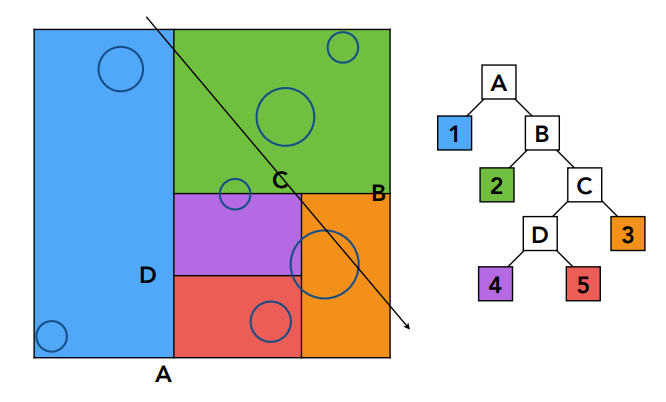
第一次判断是否与A存在交点,光线有交点则可能与左右子节点产生交集
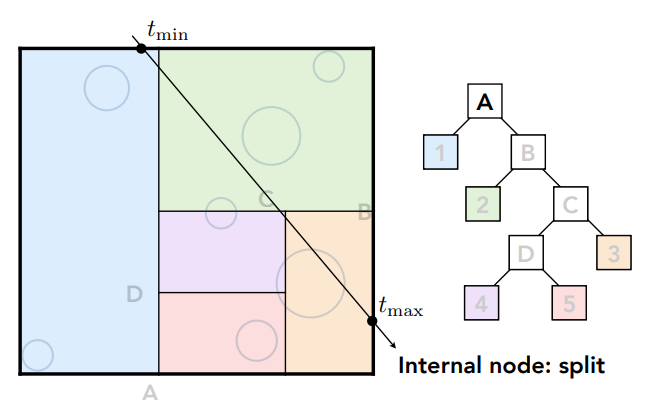
检测是否与子节点存在交点,发现与左边蓝色区域存在交点,按图中划分,1不再划分的情况下则认为光线与该叶子节点(蓝色区域内)所有物体求交
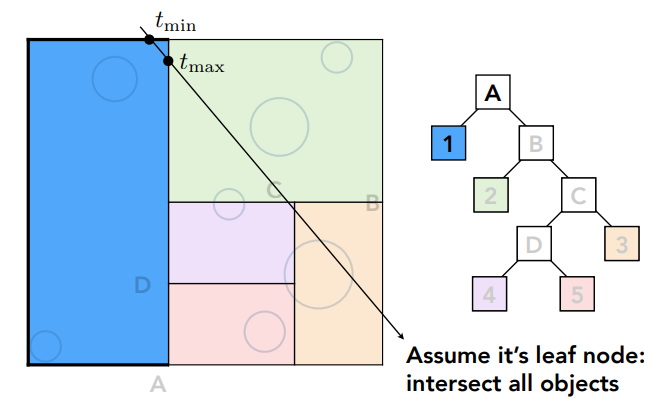
检查右子节点,发现与右边区域也有交点,则光线可能和B的子节点(2和C)相交
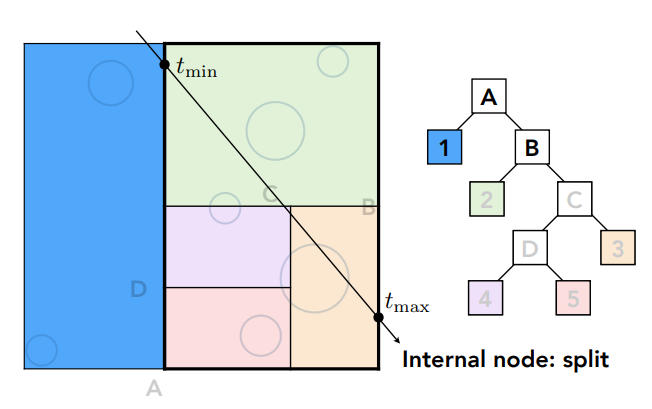
再判定光线与2和C区域相交情况,发现与2存在交点,此处假设2不再细分,2即为一个叶子节点,光线需要和2中所有物体求交
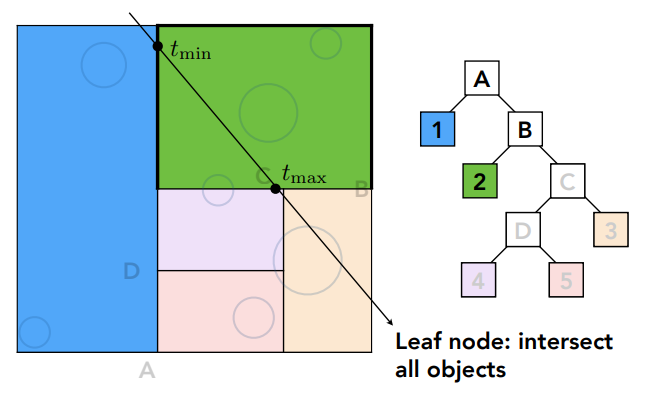
发现与C区域存在交点,那便要判断光线和C的子节点(D、3)是否有交点,发现和3存在交点,且3为叶子节点,则光线要和3中的所有物体求交,D同理,一直求到叶子节点(区域5与光线无交点,无需求交)
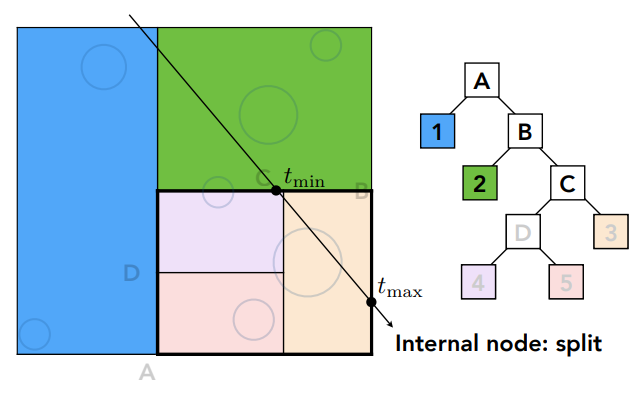
在C中光线和所有物体求交就找到了交点
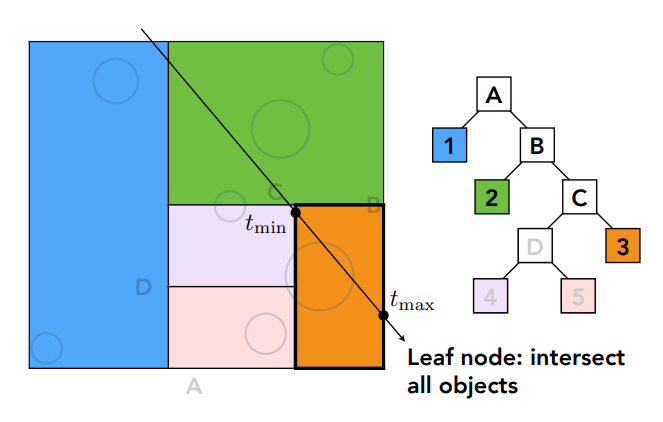
KD-Tree的问题
- 难以判定包围盒和物体的交集
虽然三角形只要有一个顶点在盒子内,就可以判定相交,但存在三个顶点都不在包围盒内但依旧相交的情况(包围盒在三角形内部)
- 一个物体可能出现在多个不同的叶子节点里
如案例中右下角的圆与3、4、5都存在交点,会在叶子节点3、4、5中存储这个物体,这会造成性能浪费
BVH(Bounding Volume Hierarchy)
BVH无论在实时的光线追踪还是离线的结构都解决了KD-Tree的问题,在图形学里有广泛地运用
BVH结构创建
同样将场景用一个盒子包围,与KD-Tree不同在于后者将物体划分为2个部分
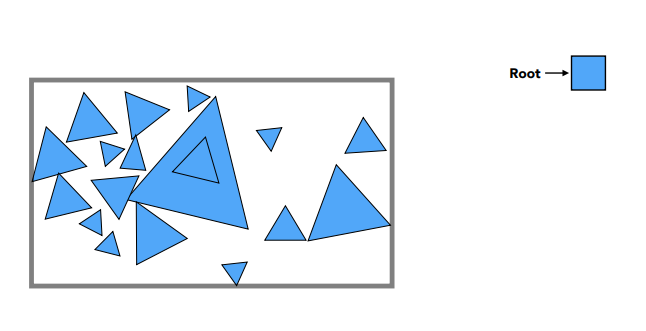
将上图方框中所有三角形分割成两个部分再重新求它们的包围盒
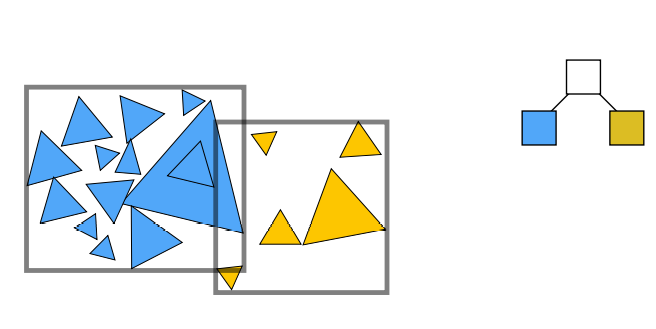
同样再继续划分,将上图蓝色节点划分为两堆三角形再重新求它们的包围盒,对应下图蓝绿节点
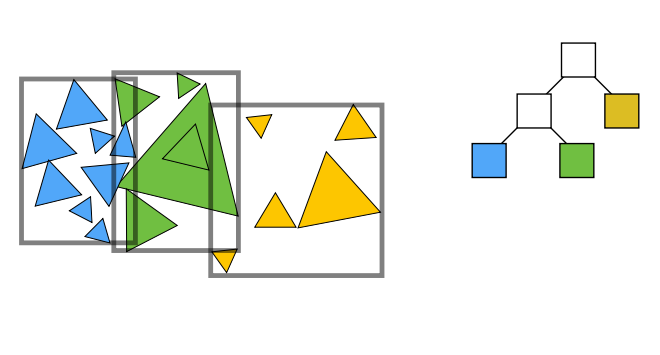
划分终止条件自定义:如一个节点中只有5个三角形存在
总结:
- 找到一个包围盒
- 基于包围盒中的物体,递归地拆分包围盒为两个部份
- 两个部份各自重新计算包围盒
- 叶子节点中三角形数量满足终止条件时停止划分,记录实际的物体至叶子节点里,其余结构用于判断加速结构
BVH性质
-
一个叶子节点里只可能出现在一个几何结构里
-
可以不采用求三角形和包围盒的交
按物体划分使得包围盒求取简易,避免了空间划分中求包围盒和物体的交集
问题:
未严格划分空间,不同的Bounding box间可以相交
BVH节点划分方式
-
与KD-Tree一样选择一个维度来划分
-
方法一:只沿着最长的轴将其分成两半
-
方法二:取中间的物体进行划分
例如:
一行三角形从左到右依次排列寻找中位数,第n/2个三角形
中位数可确保两部分数量相似即生成的树接近平衡(通过保证两边深度相似可减少平均搜索次数)
排序上可假设沿着X轴去考虑三角形,则所有三角形取重心后沿X轴排序便可得知中间的三角形位置(快速选择算法)
以上步骤可得到一个预计算的BVH,如果场景发生改动则需要重新计算
BVH的数据结构
-
内部节点存储
- 包围盒
- 指向子节点的指针
-
叶子节点存储
- 包围盒
- 实际的物体
-
节点表示场景中分割框的子集
- 子树中的所有物体
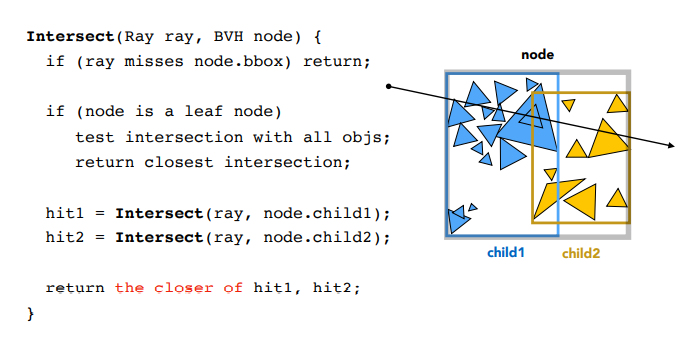
BVH与光线求交
与KD-Tree类似,光线和根节点求交,找到内部物体最近的交点
光线与BVH节点相交后存在两种可能:
- 节点本身为叶子节点,此时光线与叶子节点里所有物体求交,放回最近交点
- 节点本身不是叶子节点,此时光线可能与该节点的两个子节点都有交点,递归地求出它们的交点再返回最近的点
空间/物体划分区别
- 空间划分(Spatial partition)
- 划分空间,任何一个节点在空间和时间之间不会有交集
- 有些物体存在横跨边界的可能
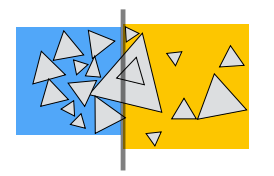
- 物体划分(Object partition)
- 划分物体,物体分为两部分后分别计算包围盒
- 包围盒存在交集的可能,但不产生影响且无需计算包围盒相交方式