几何
几何物体的表现形式
隐式(Implicit)
- 代数平面(algebraic surface)
- 水平集(level sets)
- 距离函数(distance functions)
- ...
优缺点
优点:
- 描述简洁(如,一个函数)
- 便于某些查询(判定物体内部,或内部点到表面的距离)
- 便于计算光线到表面的交集
- 对于简单的形状能够做到准确描述无抽样误差
- 易于处理拓扑变化(如,流体)
缺点:
- 难以模拟复杂的形状
基于一系列满足特定关系的点
例如:
球体:所有的点在三维坐标系里满足$$x^2 + y^2 + z^2 = 1$$或$$f(x,y,z) = 0 $$
难以采样
例如:
在一系列符合下列条件的点中,难以采样到符合$f(x,y,z) = 0$的点
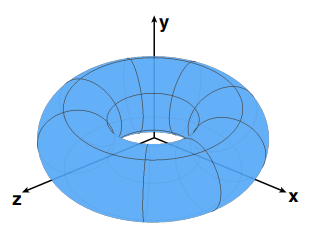
$$f(x,y,z) = (2 - \sqrt{x^2 + y^2})^2 + z^2 - 1$$
对应的几何形状如下图
易于判断内外关系
例如:
在一系列符合下述条件的点中
$$f(x,y,z) = x^2 + y^2 + z^2 - 1$$
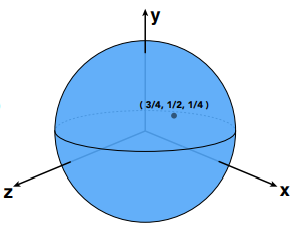
对于点$(\frac{3}{4},\frac{1}{2},\frac{1}{4})$ 若要判定其是否在该几何体内部则只需计算$$f(x,y,z) = - \frac{1}{8} < 0$$ 即可判定其位于几何体内部
代数平面(Algebraic Surfaces)
表面是x,y,z中多项式的零集

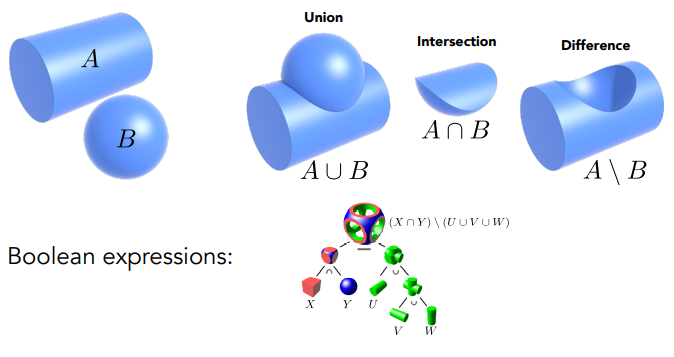
构造实体几何(Constructive Solid Geometry)
通过布尔计算组合构造隐式几何
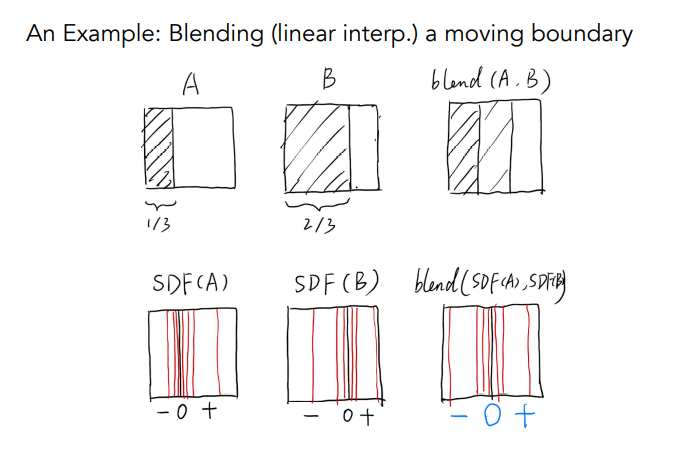
距离函数(Distance Functions)
距离函数:从任意位置到目标物体给出最小距离(符号距离)
使用距离函数将两个曲面混合在一起
水平集(Level Set Method)
封闭式的方程难以描述复杂的形状
解决方案:存储值相似的函数网格
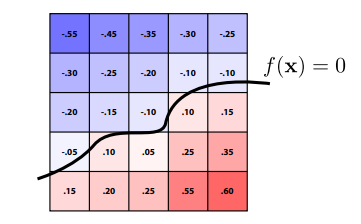
插值为零的值的位置即为表面
优势:能够提供对形状更明确的控制(如纹理)
在流体仿真中也存在应用:计算到气液边界的距离
分形(Factals)
该几何形状表现为所有尺度的细节都存在自相似性(一种描述自然现象的说法),往往难以控制形状

显式(Explicit)
- 点云(point cloud)
- 多边形网格(polygon mesh)
- 细分曲面和曲线(subdivision, NURBS)
- ...
点直接或参数映射给出
例如:
$$f:R^2 \rightarrow R^3;(u,v) \rightarrow (x,y,z)$$
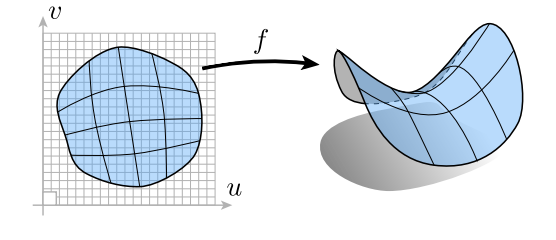
易于采样
例如:
对于$$ f(u,v) = ((2 + \cos u)\cos v,(2 + \cos u)\sin v,\sin u) $$
若要判定点$f(u,v)$是否位于表面,则只需将$(u,v)$的值相加

难以判断内外关系
例如: 对于$$f(u,v) = (\cos u \sin v ,\sin u \sin v,\cos v)$$
难以判定点$(\frac{3}{4},\frac{1}{2},\frac{1}{4})$
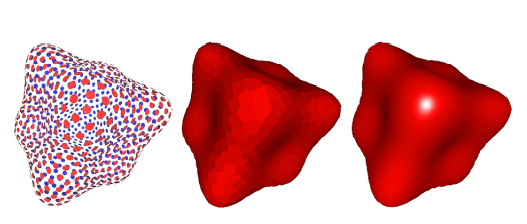
点云 (Point Cloud)
- 最简单的表示:点列表(x,y,z)
- 轻松表现任何类型的几何图形
- 适用于大型数据集(>> 1 点/像素)
- 通常转换为多边形网格
- 难以用于采样不足的区域
多边形网格(Polygon Mesh)
- 存储顶点和多边形(通常是三角形或四边形)
- 更易于进行处理/模拟,自适应采样
- 更复杂的数据结构
- 图形中最常见的表示形式

表现形式应根据目标几何模型选择最合适的类型,没有最好的表现形式

贝塞尔曲线(Bézier Curves)
定义
贝塞尔曲线完全由其控制点决定其形状,$n$个控制点对应着$n-1$阶的贝塞尔曲线,并且可以通过递归的方式来绘制.
de Casteljau Algorithm(图形)
假设存在三个点(quadratic Bezier)
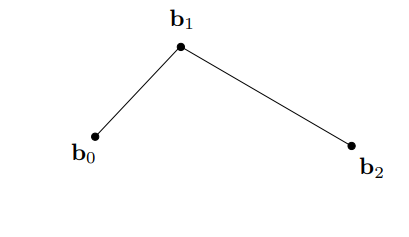
通过线性插值的方式插入一个点
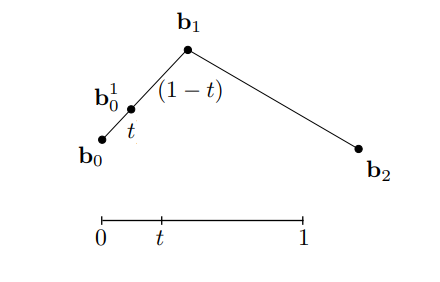
在另一边也通过同样方式插入一个点
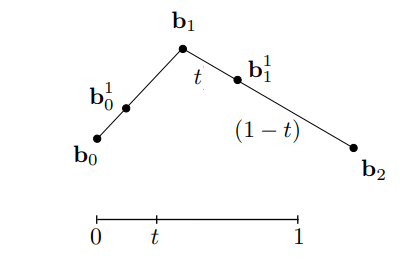
递归重复
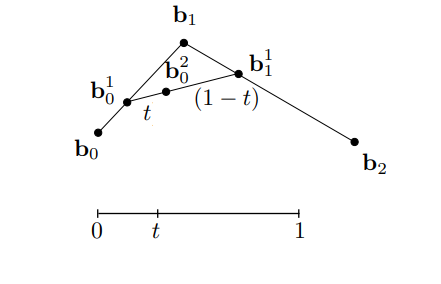
对于在$[0,1]$区间的每个t点都使用相同算法进行计算
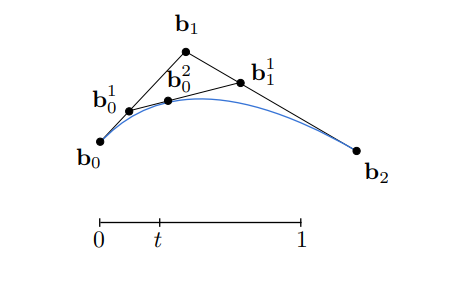
构造一个三次方贝塞尔曲线需要总共四个输入,都递归使用线性插值
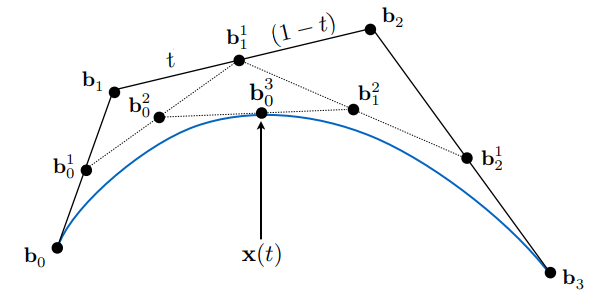
可视化算法流程
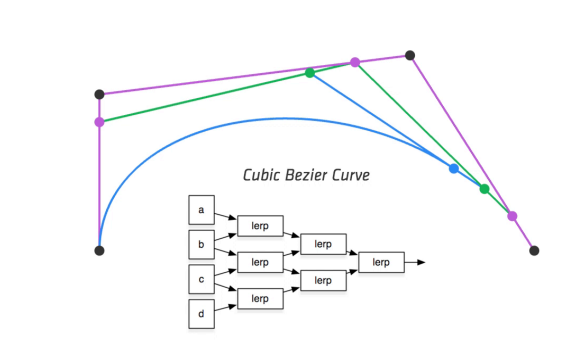
de Casteljau Algorithm(数学公式)
de Casteljau 算法给出各点间金字塔型的变量关系
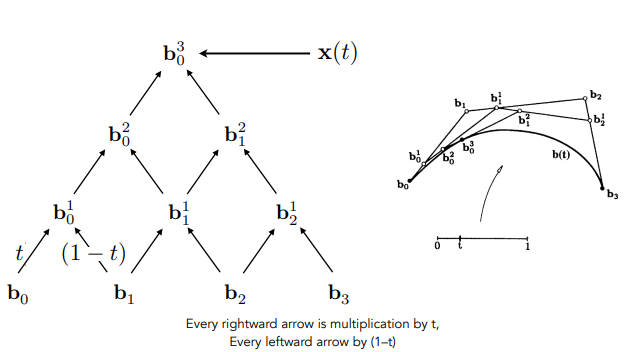
推导流程

$$b_0^1(t) = (1 - t)b_0 + tb_1$$ $$b_1^1(t) = (1 - t)b_1 + tb_2$$ $$b_0^2(t) = (1 - t)b_0^1 + tb_1^1$$ $$b_0^2(t) = (1 - t)^2b_0 + 2t(1 - t)b_1 + t^2b_2$$
进而推得$n$阶贝塞尔曲线的公式为:
$$b^n(t) = b_0^n(t) = \sum_{j=0}^{n} {b_j B_j^n(t)}$$
$b^n(t)$:贝塞尔曲线阶级数n(n次向量多项式)
$b_j$:控制点($R^N$的向量)
$B_j^n$:伯恩斯坦多项式
伯恩斯坦多项式(Bernstein polynomial):
$$B_i^n(t) = \begin{pmatrix} n \\ t \end{pmatrix} t^i(1 - t)^{n - i}$$
例如$n = 3$时
我们在三维空间里有下列控制点
$b_0 = (0,2,3),b_1 = (2,3,5),b_2 = (6,7,9),b_3 = (3,4,5)$
这些点定义了以下列公式形式的贝塞尔曲线
$$b^n(t) = b_0(1 - t)^3 + b_1 3t(1 - t)^2 + b_2 3t^2(1 - t) + b_3 t^3$$
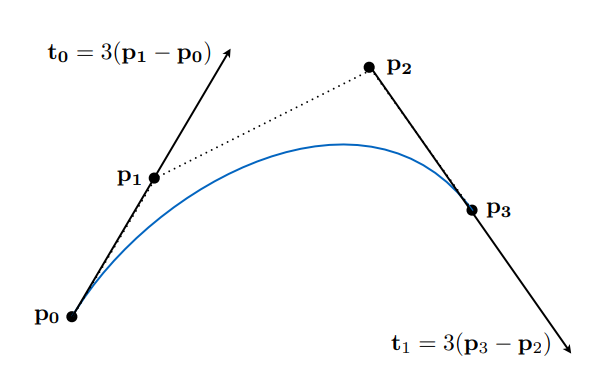
贝塞尔基本函数
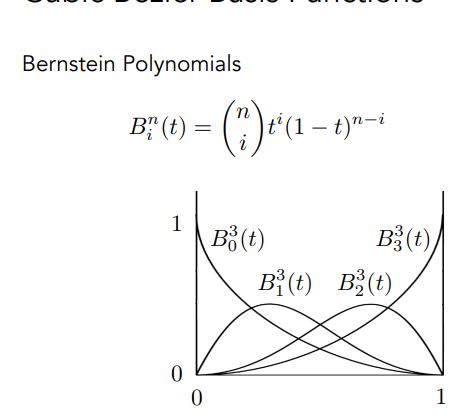
插值端点:$b(0) = b_0;b(1) = b_3$
与末端线段相切:$b'(0) = 3(b_1 - b_0); b'(1) = 3(b_3 - b_2)$
能够通过控制点的位置来改变曲线
分段贝塞尔曲线
出现原因:高阶贝塞尔曲线有多个控制点,难以控制曲线形状
对策: 将多个低阶的贝塞尔曲线相连,构造为分段贝塞尔曲线
常用于:字体,路径,插画,主题演讲
样例:
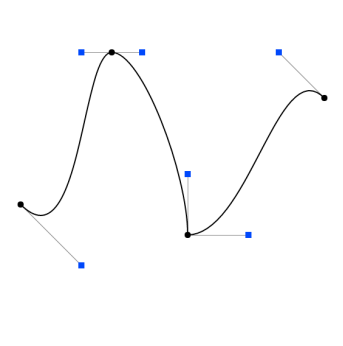
组合计算
要将一下两条贝塞尔曲线组合在一起则
$$a:[k,k+1] \rightarrow IR^N$$ $$b:[k+1,k+2] \rightarrow IR^N$$
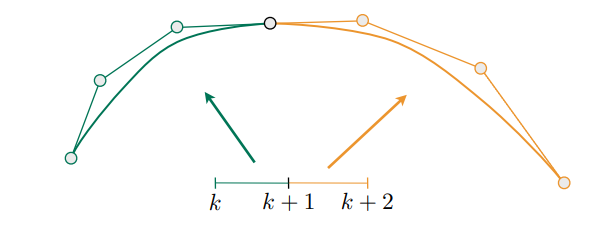
$c^0$处的连续性:$a_n = b_0$
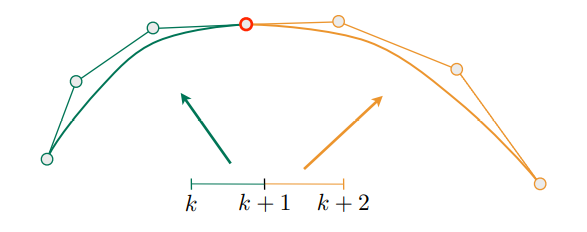
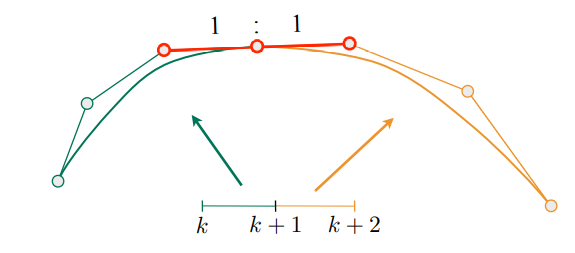
$c^1$处的连续性:$a_n = b_0 = \frac{1}{2}(a_{n-1} + b_1)$
贝塞尔表面(Bézier Surfaces)
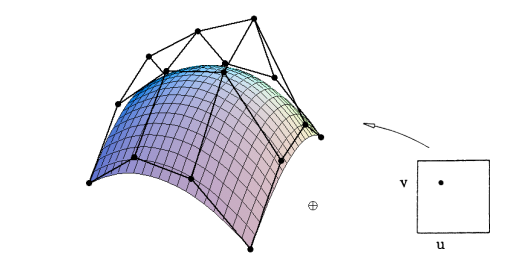
对于一个双立方贝塞尔表面贴片
输入:$4 \times 4 $ 控制点
输出:由$[0,1]^2$ 参数化的2D平面
计算方法
目标:计算相对于(u,v)的平面位置
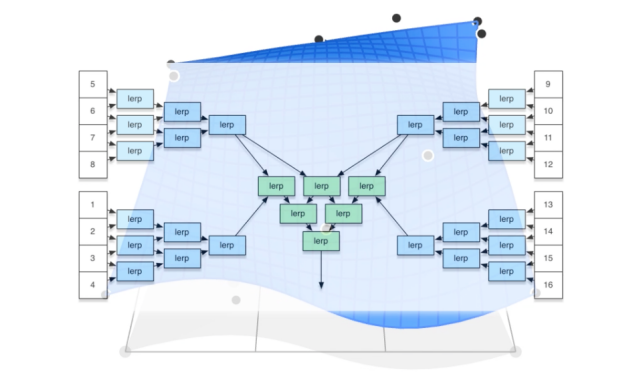
- 使用 de Casteljau 算法来计算四条贝塞尔曲线上各自的U,这将会为"移动"贝塞尔曲线提供4个有效的控制点
- 使用一阶 de Casteljau 算法来计算"移动"曲线上的点V
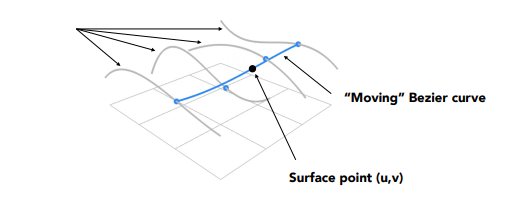
可视化计算流程:
曲面处理(Mesh Operations)
曲面细分(Mesh Subdivision)
目的:提高分辨率

通常做法:
- 创建更多三角形(顶点)
- 更新它们的位置
Loop Subdivision
- 将每个三角形划分为4个三角形
- 根据权重更新顶点的位置(新旧顶点各自以不同方式进行更新)
新顶点:
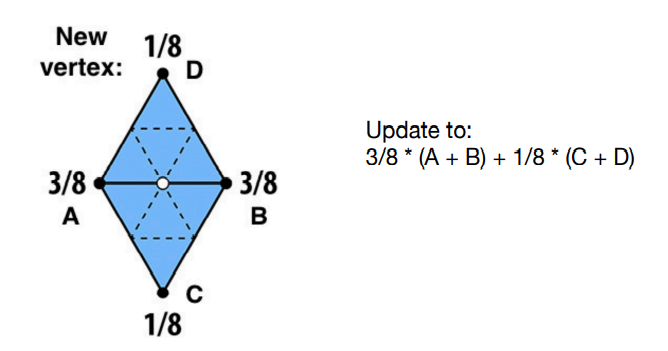
白点即为新顶点,其位置为周围四个顶点的权重之和
旧顶点:
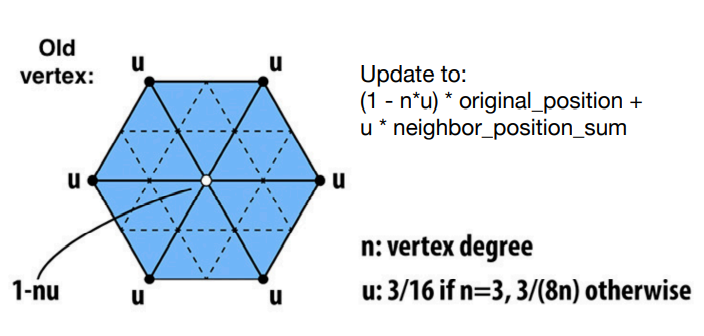
白色旧顶点也是自身及邻接顶点的权重之和,权重的设置与旧顶点度数关联
Catmull-Clark Subdivision
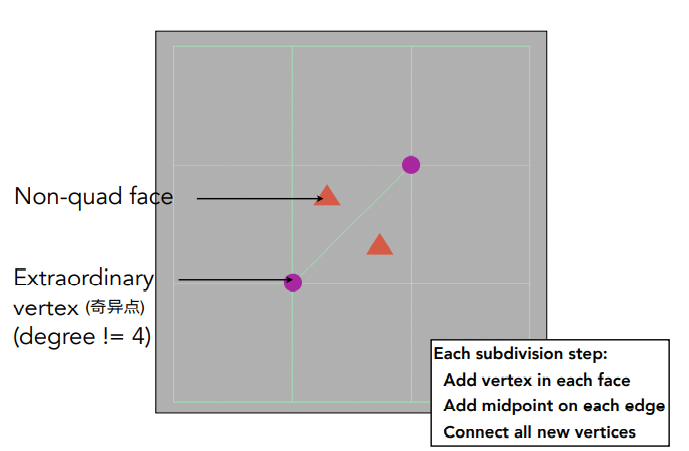
定义:
- 所有非四边形的面都称为Non-quad face
- 所有度不为4的点称为奇异点
- 每次细分时在每个面中添加一个点,每条边的中点也都添加一个点,面上的新顶点连接所有边上的新顶点
第一次细分后结果:

特点:
- 非四边形面的数量与奇异点相同,即现在共有$2+2=4$个
- 奇异点的度数与原来所在面的边数相等,即这里为3度
- 第一次细分后所有的面都会变成四边形,且后续奇异点数目不再增加
Catmull-Clark 顶点更新规则
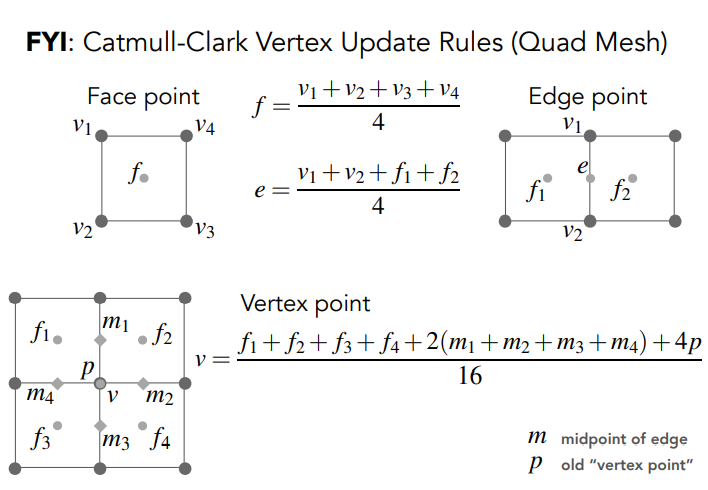
收敛性:整体形状和折痕
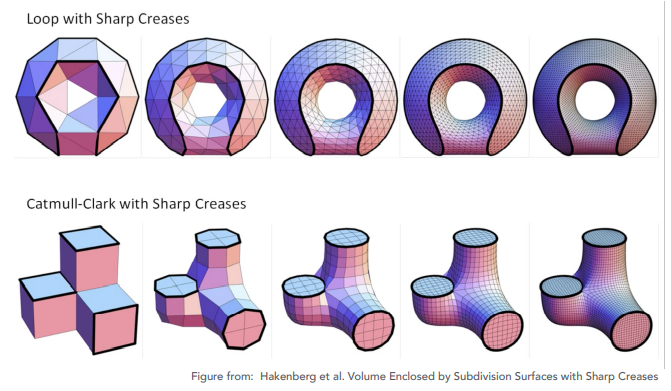
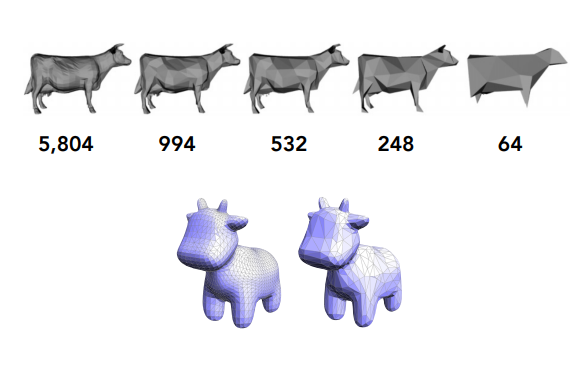
曲面简化(Mesh Simplification)
目的:降低分辨率的同时尽量保持形状/外观

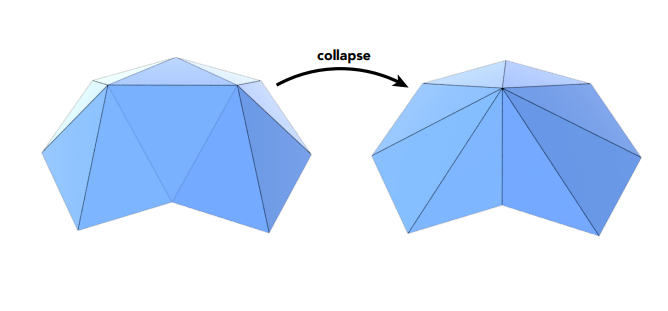
边坍缩
边坍缩是曲面简化的常用方法,如上图所示将一条边的两个顶点合成为一个顶点,出于尽量保持形状的目的,需要正确选择不影响或影响最小的边进行坍缩,由此引入二次误差度量(Quadric Error Metrics)
二次误差度量(Quadric Error Metrics)
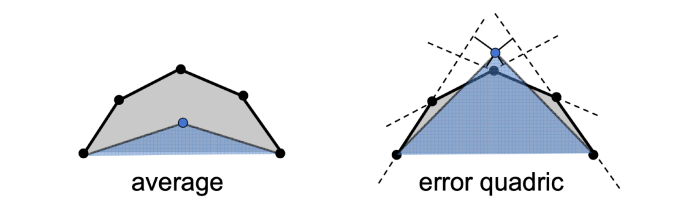
坍缩之后蓝色新顶点所在位置与原来各个平面的垂直距离之和,如此误差最小则整个模型样貌修改一定程度也会较小
曲面简化算法流程
- 为模型每条边赋值,其值为坍缩后代替老顶点产生的新顶点所得到的最小二次误差
- 选取权重最小的边做坍缩,新顶点的位置为原计算得出使二次误差值最小的位置
- 坍缩之后,会改动与之相连的其他边,更新这些边的权值
- 重复步骤,直到符合终止条件
符合贪心算法标准,无法获得最优解,但效果依旧合适
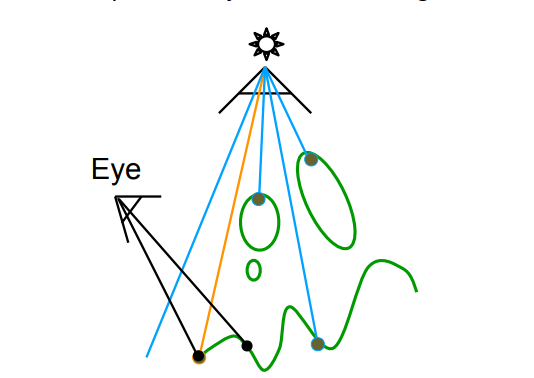
纹理映射(Shadow Mapping)
Shadow Mapping是一种基于图像的算法
- 阴影计算期间无需进行几何体计算
- 必须进行反走样处理
- 不在阴影中的点必须同时在灯光和相机范围内
计算流程
阴影映射总体需要两个pass
Pass1:render from light
- 获得从光源视角得到的深度图像
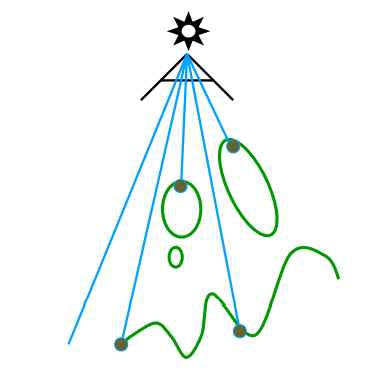
Pass2:render from eye
- 从观看视角(相机视角)获得带有深度的标准图像
- 将观看视角中的可见点投影回光源
- 光源和观看视角的下的深度相同时为可见
- 光源和观看视角下的深度不相同则为被阻挡