动画:
- 交流工具,用于展示会动的东西
- 关注美学,早期动画是绘画制作的,不关注物理是否符合现实,只要看起来正确
- 建模或几何的拓展:动画即为在不同时间或不同帧有不同几何形状,将3D模型延伸到时间维度
动画生成:
将很多图形按一定顺序和速度播放
- 电影:一秒播放24帧
- 视频:30帧每秒
- 游戏:体验好需要60帧甚至144帧每秒
- 虚拟现实:防止用户产生眩晕需要两眼画面90帧每秒
动画发展历史
- 远古人类壁画

- 圆盘转动
人们人为制造的可以看到的动画
最早起,有类似圆盘的物体,可固定在某处,可以旋转

- 第一部电影
早期不用于娱乐,是一种科学研究的设备,如下图拍摄奔跑中的马可用于研究马匹运动时四肢动态

- 第一部与电影时长相当的动画
第一部手绘的与电影时长相当的动画,即剧场版:白雪公主和七个小矮人
每秒播放24帧,制作耗时极长

- 第一部计算机生成的动画
可追溯至1963年

- 早期计算机动画
如下图为人脸的三维结构网格,已经可以做到人物面部表情

- 电子(计算机生成)恐龙(Digital Dinosaurs)
如下图,侏罗纪公园,真正将计算机生成的恐龙放入电影中

- 第一部计算机生成的电影时长动画
第一部完全用计算机生成的动画电影:
皮克斯的《玩具总动员》
采用光栅化的方式生成阴影效果

- 十年前的计算机动画
依旧缺少一些细节

- 2019-冰雪奇缘2
充满各种细节

关键帧动画
下图中,上面一行的3个动作是重要位置,对应的帧称为关键帧
下面一行在2个动作间补充过渡的动作
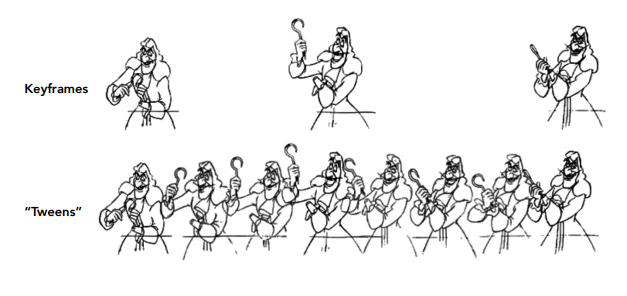
关键帧插值
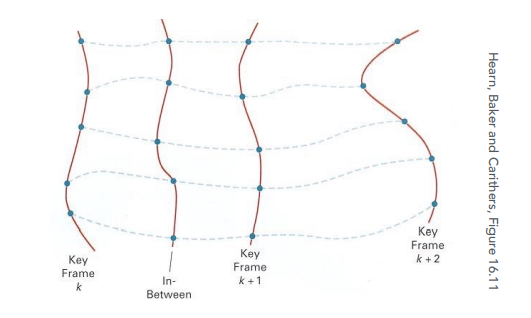
给定一系列不同的帧,中间帧采用插值的方式计算得到
找出每一帧中重要的点在其他帧的位置,所有点一一对应找出后就可以插值计算得到结果
插值得到的过渡往往需要看着自然、真实,对插值方式有一定要求
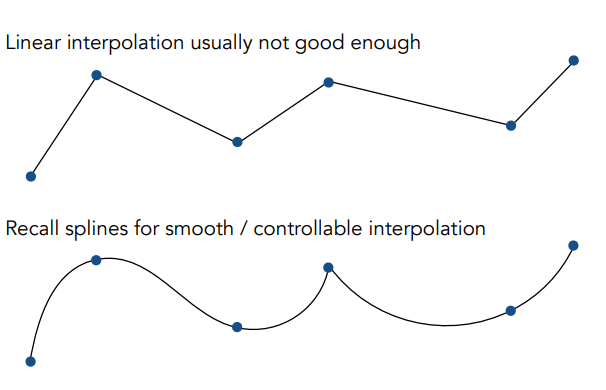
最简单的是线性插值,但下图为非线性插值
线性插值:
给定任意的连续点,将其连接成线段
有时需要更好的连续性,就需要用到曲线和样条,这说明几何和动画之间时存在联系的
物理模拟
关键字动画是最简单的方式,插值方式生成中间帧,但人们往往更常用物理仿真的方式
牛顿运动定律
$$F = ma$$
F: 施加在物体上的力
m:物体的质量
a:物体的加速度
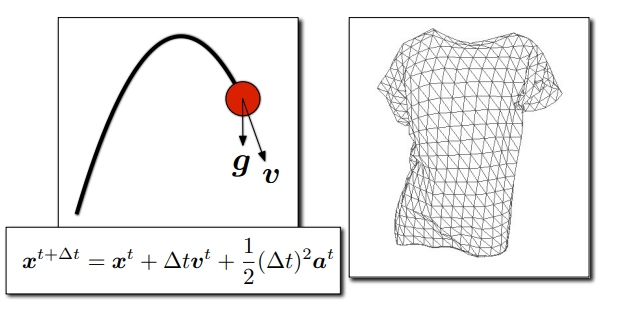
- 小球在重力影响下抛出时会形成抛物线
- 衣服可认为由网格形成,任何一个顶点有一定质量,受重力影响,也受其他点作用的力的影响
案例
- 布料模拟

- 流体仿真
- 模拟水的运动和水滴的形成位置
- 模拟了位置和形状后进行渲染得到样式

质点弹簧系统
案例
- 绳子模拟
将一根绳子模拟成很多小的弹簧,允许其在重力作用下来回摆动

- 头发

- 布料
布料是由网格描述的,可以使用各种不同的质点弹簧系统描述,还可使用一个点进行拖拽
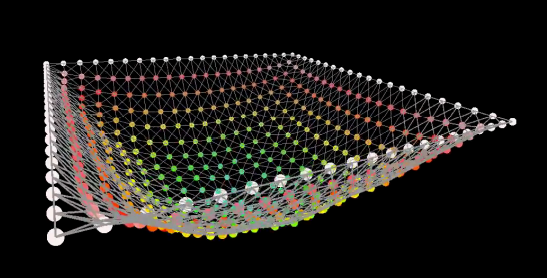
建模足够好的情况下,模拟与仿真可以做到与现实几乎一致

上图受限于PDF,建议结合games101第21课
简单的质点弹簧系统
-
质点弹簧系统:一系列相互连接的质点和弹簧
-
最基础的单元:一个弹簧两侧连着两个质点
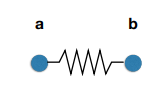
- 理想的弹簧(无长度,产生的力与被拉长的长度成比例)
$$f_{a\rightarrow b} = k_s(b-a)$$
$$f_{b\rightarrow a} = -f_{a\rightarrow b}$$
- $f_{a\rightarrow b }$为应用到a上,往b方向的作用力,往往取决于a和b之间的距离
- (b-a)为从a指向b的向量,b-a越长,力越大,可以写出a点往b点的力
- $k_s$劲度系数(胡克定律:固体材料受力后,应力与形变量之间存在线性关系)
- 因为力的作用的相对性,a受到向右的力,b肯定受到向左的力,两者互为相反
- 非0长度弹簧
弹簧在正常情况下有一定的长度,为Rest length
弹簧在拉伸后
- b和a的距离为$||b - a||$
- 形变量为$||b - a|| - l$
- 受力的方向$\frac{(b - a)}{||b - a||}$
$$f_{a \rightarrow b } = k_s \frac{b - a}{||b - a||}(||b - a|| - l)$$
因能量守恒,会永远振动下去
- 加入摩擦力
平常我们会用x来表示位置,x的一阶导数(x′)表示速度,x的二阶导数(x′′)表示加速度,在物理模拟中会用x上面加一个点表示速度,加2个点表示加速度
$$\dot{x} = v$$
$$\ddot{x} = a$$
加入摩擦力(damping force)使它能停止
对于任何一个运动的质点,如果想让它停,那力的方向肯定和速度方向相反
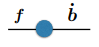
问题:
会引起所有的运动都停下来,这样描述的摩擦力只能描述外部的力,描述不了弹簧之间内部的力
- 加入内部摩擦力
目的:希望弹簧恢复到正常长度
方向:$-(b - a)/||b - a||$
大小:下图红框部分,a和b之间的相对速度投影在ab方向上的速度
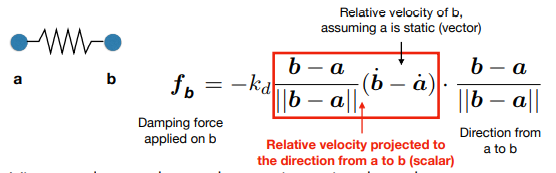
弹簧结构
弹簧可以组合成各种形状
如下图,可以每2根共用一个质量表示一张平面,也可以在三维空间中进行连接
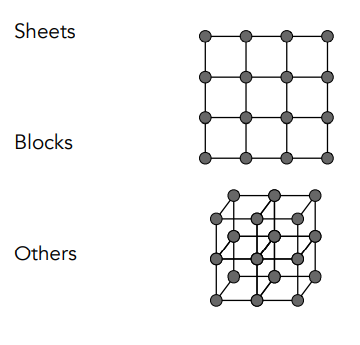
使用各种弹簧模拟一块布
- 问题1:切变会受影响
- 问题2:存在一种力让整个形状变得不是一个平面
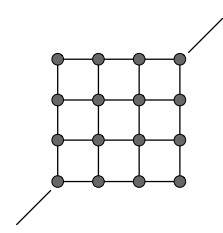
- 加入斜的对角线解决切边
在以上的形状中加入斜的对角线,发生切变时,新加的蓝线会被压缩,那弹簧就会向外抵抗它
存在结构不对称问题,无法使模拟的布在任何一个方向拉它,它的行为保持一致
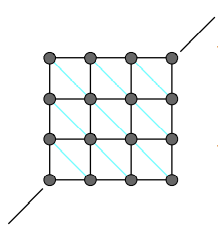
- 加入另外一个方向上的斜对角线
不能抵抗非平面的弯曲(沿着竖的或横的线折叠)
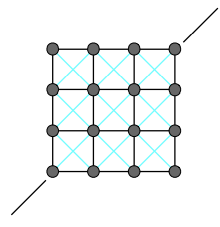
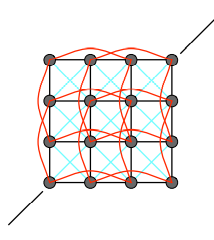
- 加上跳过相邻质点的连接线
如下图的红线,任何一个点都和它隔一个点连一根线
红线的连接是非常弱的,蓝线非常强
- 例子
下图是质点弹簧系统做的裙子
简化的表示,未表示纤维、股和线等之间的力的关系

- 拓展
除了质点弹簧系统,还有其他的方法,比如有限元方法(FEM (Finite Element Method)),这个方法被广泛应用于车辆碰撞,能够表现力之间的传导作用

粒子系统
用于描述一些很小很小移动的东西
建模一堆很微小的东西,定义每一个粒子会受到的力(有重力、风力、粒子和粒子之间的力)
很容易模仿一些魔法效果、雾、灰尘等等
粒子越多模拟得越精细,但是越慢;越少,计算速度越快,但效果差一些

存在问题
- 粒子系统可以模拟流体,这样可能需要很多粒子
- 粒子和粒子之间的作用不只有碰撞,还可能有引力,需要随时更新粒子的位置
算法
- 动态生成一些新的粒子
- 计算每个粒子的作用力
- 根据作用力更新粒子的位置和速度
- 如果粒子有存活时间,移除消亡的粒子
- 渲染粒子
粒子系统的力
- 吸引力和排斥力
- 重力、电磁力
- 弹力、推力
- 阻尼力
- 摩擦力、空气阻力、粘滞力
- 碰撞
- 墙、容器、固定物体
- 动态物体、角色身体碰撞
例子
- 万有引力
最小的物体都会满足此规律
$$F_g = G\frac{m_1m_2}{d^2}$$
$$G = 6.67428 \times 10^{-11}Nm^2kg^{-2}$$
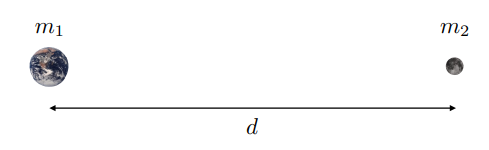
- 银河模拟

- 基于粒子的流体模拟
模拟的是粒子,渲染的是像玻璃、是否带白沫

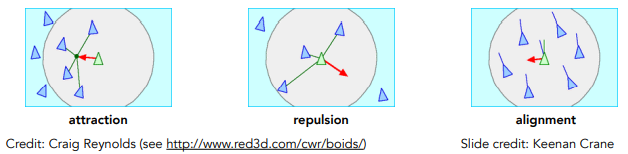
粒子间相互作用
粒子系统不一定只是描述最简单的点,这个粒子也就是在一个很大范围内有很多重复的东西
个体的运动属性:
会被中央的相邻点吸引
粒子间间隔不会太近
所有粒子会对齐一个方向
有了以上的属性就可以通过粒子的方法解出来
- 分子结构

- 人群

运动学
在图形学中运动学分为正向的和反向的,即正运动学和逆运动学
正运动学
骨骼系统
用于描述和人骨骼连接拓扑结构类似的结构,可定义不同的关节
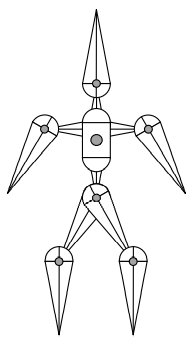
- Pin
钉子钉住后只能在钉住的平面内往一个方向旋转
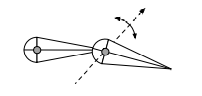
- Ball
有一个东西可以包住一个球,这个球可以任意的在任意方向旋转
- Prismatic joint
可以拉长,也就是可以有一些移动
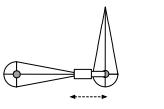
一个简单的关节
如下图,只能在平面内发生旋转,类似于肩和肘的旋转,假设第一段旋转$\theta_1$度,第二段旋转$\theta_2$度,如何确定尖端位置
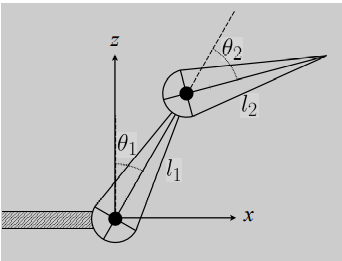
先算出上方黑点的位置,因为$\theta_2$是在$\theta_1$的基础上旋转的,可以用$\theta_1$加$\theta_2$计算
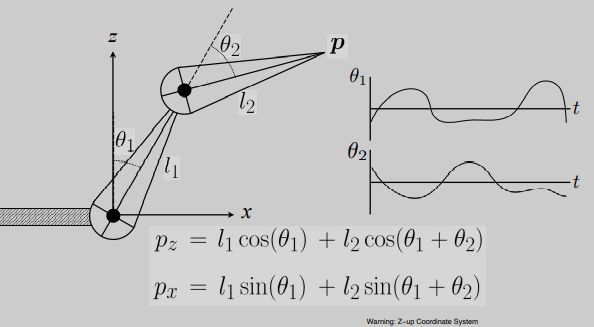
因此,正向运动学需要定义好连接方式,定义好它们之间的各种位置,就可以找到各种点的位置
- 例子
人类行走动作模拟

优缺点
- 优点
实现容易
- 缺点
它的定义都很物理
但是艺术家们更喜欢直观的控制尖端进行动画的创建,而非调整角度
逆向运动学
逆运动学可以手里捏着尖端到处移动,它会自动的调整它的关节的位置,使得尖端就在你要的位置上
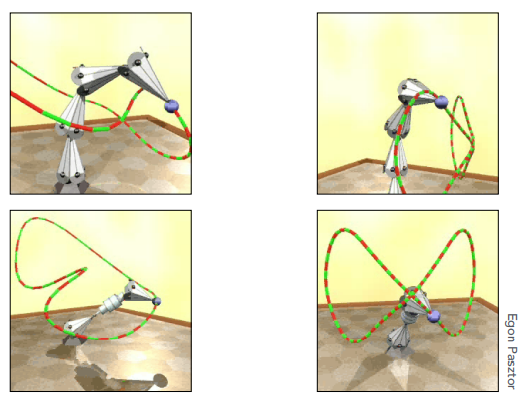
如下图中,给出固定点P,它就会给出$\theta_1$和$\theta_2$,解出这两个角度的过程比较复杂
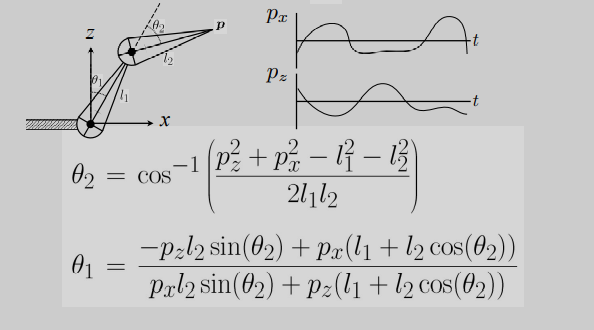
问题
- 逆向运动学的解有时候不唯一
如图,尖端位置确定,但存在两个解
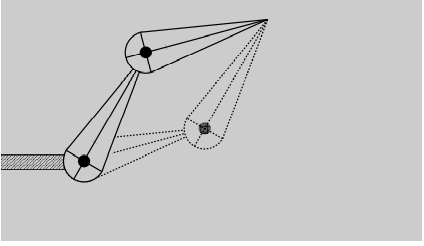
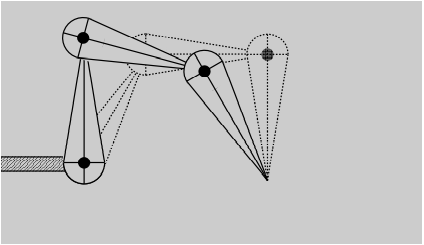
- 存在无解的情况
最上面的关节点只可能出现在下图的虚线上,尖端通过旋转可以在一个圆上,从而尖端只有可能在外层的圈和内层的圈之间,其他位置到不了
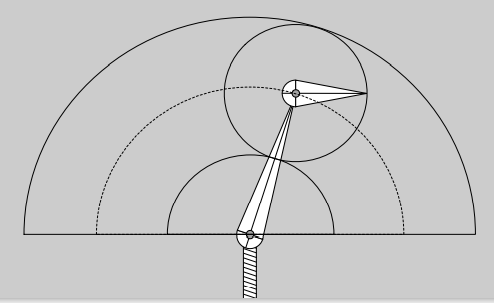
问题优化
一般N维IK问题的数值求解
- 选择初始配置
- 定义错误度量(例如:目标与当前位置之间距离的平方)
- 计算误差梯度作为配置的函数
- 应用梯度下降或牛顿方法
绑骨(Riging)
对于一个形状的控制,其实就是木偶操作,一定程度上就是逆运动学的一个应用
例子:
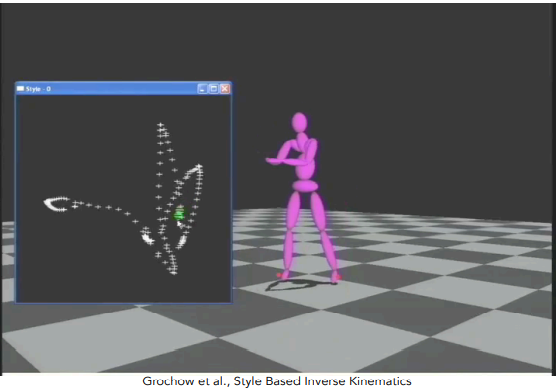
形状混合
人物有2个不同的动作,这2个动作之间可以通过插值的方式做。利用控制点做了2个不同的造型,然后将控制点和控制点之间的位置做插值
实际为混合控制点及其影响区域

动作捕捉
给真人各个不同的地方加上控制点,让这些控制点的位置直接反应到虚拟的造型上去。要建立虚拟的人物和真实的人物之间的关系,此时只要人在做动作时将它拍下来,就可以知道控制点的不同的位置并反应到对应的人物上面去

优缺点
- 优点
可以迅速捕捉大量的真实数据,避免手K的耗时耗力的操作
真实感非常强
- 缺点
进行动作捕捉需要很多前期的准备
捕捉出来的动作可能不符合艺术家的需求,需要调整(比如真人去演动画人物,动画人物的表情是很夸张的;或者有时捕捉不到好的数据,比如捕捉条件有限制,人在正面的时候看到的控制点,背面也有但正面看不到,那就要在背后加一个摄像机,这就需要成本,而且正常需要更多的摄像机;人物动作的时候还会遮挡)

其他捕捉方法
还有磁力的(不受遮挡影响)、机械的(真正在人身上贴上机械的东西)

光学动作捕捉
应用最广泛的还是光学的捕捉方法,贴一些Maker(贴片或小球)贴在人身上,然后用很多很复杂的摄像机,将这些点的位置非常准确的测出来


获取的动作数据
下图曲线就为一个控制点不同时间在三维空间中的位置
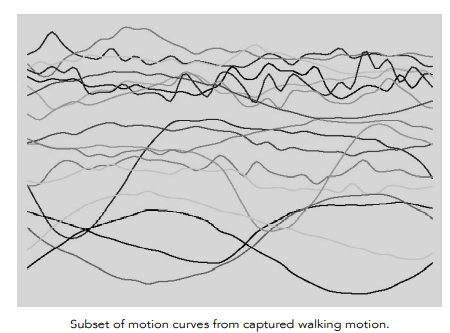
面部动画的问题
非常真实的动画往往会出现恐怖谷效应
恐怖谷效应:人们会对生成的过于真实的人类感到害怕

面部动作捕捉
阿凡达这部电影具有里程碑式的效应,就是因为使用了面部动作捕捉
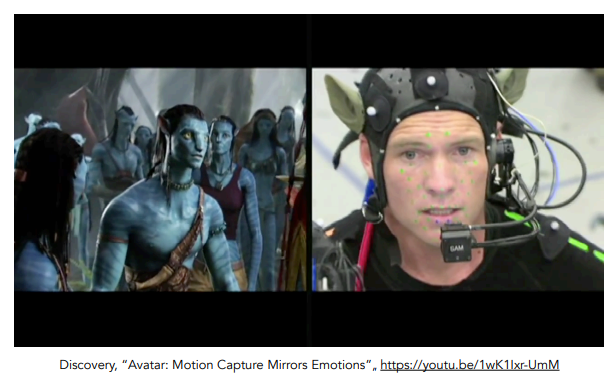
动画/电影的生成过程
分别为Pre-Production、Production、Post-Production三个部分,具体工作内容和职责可由下图所示
单粒子模拟
可在已知任何一个物体任何时刻的速度和初始位置的情况下计算某个时间后的位置
- 粒子满足匀速直线运动,初始位置加上速度和时间的乘积即可
- 一个粒子在一个速度场会沿着类似水流的方向往前走
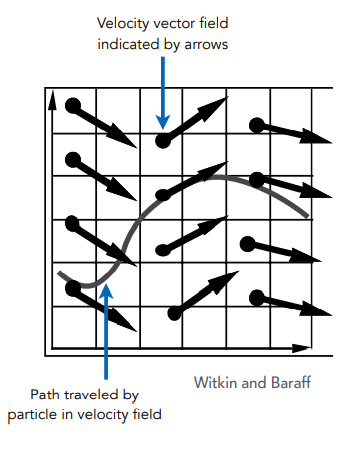
此时在任何一个位置x和时间t,都有一个速度
$$v(x,t)$$
常微分方程(ODE)
对于一个物体的运动模拟,可以写成一阶常微分方程(Ordinary Differential Equation (ODE)的形式
$$\frac{dx}{dt} = \dot{x} = v(x,t)$$
欧拉方法(前向欧拉,显式欧拉)
已知速度和起始位置,求任意时刻位置
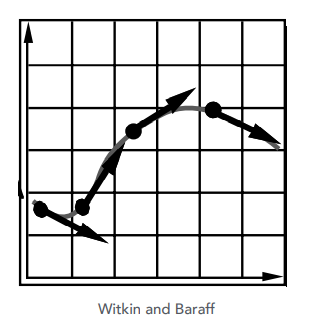
将时间细分为很多的小块,不断计算$t+\Delta t$的位置
$$x^{t+\Delta t} = x^ t+\Delta t \dot{x}^t$$
$$\dot{x}^{t+\Delta t} = \dot{x}^t + \Delta t \ddot{x}^t$$
始终使用上一时刻的量来估计下一时刻的量
问题
欧拉方法会迅速变得不稳定
- 减少$\Delta t$来减少误差
$\Delta t$分得越细,模拟就会越精确,如果越大,和实际的路线偏离得越多
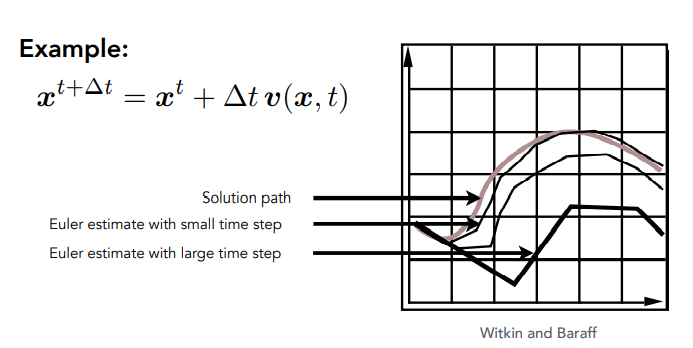
- 不稳定性
不稳定:无论取多大的$\Delta t$,它都会变得和实际结果相差无限远
如下图,不管取多大的步长,路线都肯定不会沿着螺旋形走,而且一定会离开这个螺旋形的速度场
事实上,粒子在一个螺旋形的速度场,一定会按照严格的圆周运动
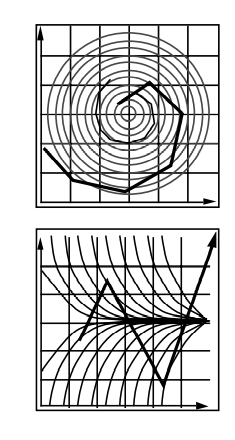
如下图速度场中,粒子运动轨迹与实际按一根曲线慢慢走到水平存在极大差别
总结:数值方法解微分方程都会面临的问题
- 误差
每一步计算都会有误差,累积起来还是有误差
如果用的步长较小,就可以降低误差
对于图形学来说,有时候模拟出来的误差问题也不大,因为图形学关注的是模拟看起来的效果,而不是物理上特别的真实
- 不稳定
不管通过怎样的方法模拟得到的结果,最后都和实际的正确的结果差得越来越远
如下图对应链接的视频,在绝地求生中,车辆撞上摩托后会出现奇怪的翻滚现象,这在许多存在物理引擎的游戏中普遍存在

解决办法
- 中点法
避免欧拉方法在模拟的过程中让结果离得越来越远
- 一开始有一个位置和一个方向,可以直接用欧拉方法来模拟某个$\Delta t$,让其先到达a
- 取原始点和a点之间的中点b,考虑它所在的速度
- 再回到原始的出发点,应用b点的速度来重新再算一遍欧拉方法,到达c点
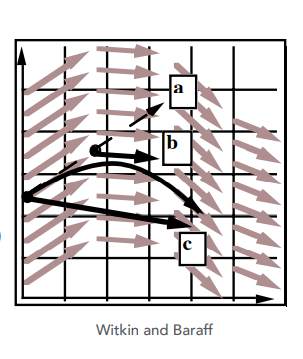
$$x_{mid} = x(t) + \Delta t/2 \cdot v(x(t),t)$$
$$x(t+\Delta t) = x(t) +\Delta t \cdot v(x_{mid},t)$$
依旧使用的欧拉方法只是计算了两次,第一次得到中点速度,第二次代入中点速度计算
因为多了一个二次项而更加准确
$$x^{t+\Delta t} = x^t +\frac{\Delta t}{2}(\dot{x}^t+\dot{x}^{t+\Delta t})$$
$$\dot{x}^{t+\Delta t} = \dot{x}^t + \Delta t \ddot{x}^t$$
$$\dot{x}^{t+\Delta t} = x^t +\Delta t \dot{x}^t + \frac{(\Delta t)^2}{2}\ddot{x}^t$$
可以认为中点法作为修正的欧拉方法算出了局部的二次的模型,因而比一次的模型准确
- 自适应步长改变
如图,原始点使用欧拉方法经$\Delta t$在$x_T$上
将时间减半,得到2个$\Delta t$,计算2次,从原始点先用$\frac{\Delta t}{2}$ 算到一个位置,再使用$\frac{\Delta t}{2}$再算一次,到达$\frac{x_T}{2}$
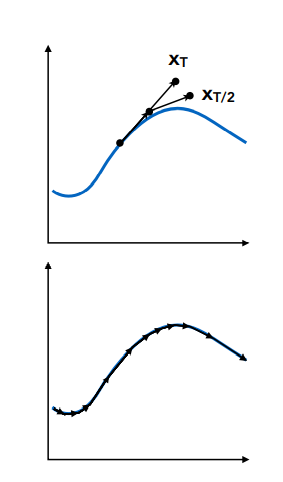
如果$x_T和\frac{x_T}{2}$这2个点差得挺远,这就意味着将$\Delta t$分成2部分分别考虑这样做会更准确,那就应该考虑$\frac{\Delta t}{2}$;如果差得不远,就没必要再分下去
- 隐式欧拉方法
使用下一个时间的梯度来更新此时
要解下列方程组,如果速度与加速度之间不是简单的线性关系就不太好解了
$$x^{t+\Delta t} = x^t +\Delta t \dot{x}^{t+\Delta}t$$
$$\dot{x}^{t+\Delta t} = \dot{x}^t+\Delta t \ddot{x}^{t+\Delta t}$$
可以用求根公式,虽然比之前数值的解法要慢很多,但隐式的方法可以提供更好的稳定性
- 龙格库塔方法(Runge-Kutta Families)
龙格库塔是一类解常微分方程(ODE)方法(特别是非线性的情况)
其中RK4方法是应用最广泛的
解决的方法和欧拉方法是一样的:
有一个一阶导数,它和时间和位置有关,并且有一个初始情况
在更新的时候稍微有点不一样:用上一帧的位置用$\Delta t$乘以某个平均值来更新
下面的4个值是不同位置和不同时间在速度场中的值

非物理方法
通过调整它的不同位置,使得它最后能够满足某种限制
优点:
实现起来快、简单
缺点:
有时不能保证能量守恒的性质
刚体模拟
刚体不会发生形变,它会让内部所有的点都按照同一种方式去运动
如下图,一个刚体的位置、朝向、速度、角速度分别对时间求导后得到速度、角速度、加速度、角加速度
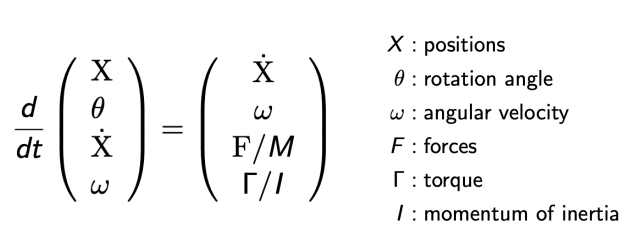
流体模拟
简单的非物理方法
通过模拟形成水的体积的小球的位置来模拟整个水的运动
- 认为整个水体是由很多不可压缩的刚体小球组成的
- 水在任何地方都是不可压缩的
- 给定任何一个时刻这些小球它们分布,都可以知道任何一个地方的密度。如果有任何一个地方的密度变得和水一开始平静的时候的密度不一样,那就需要通过移动小球的位置把这个密度修正
- 需要知道任何一个点它的密度对所有的小球位置的梯度(导数)

欧拉方法和拉格朗日方法
物理模拟中模拟大规模的物质
- 拉格朗日方法俗称质点法
模拟水是认为水是由很多圆形的小水滴组成,挨个模拟小水滴
如下图,如果模拟一群小鸟的移动,就只关注某一只
- 欧拉方法俗称网格法
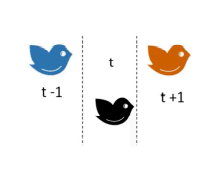
这里是指如何去看待模拟的一系列大规模的物体,将整个空间分成不同的网格,不管网格中的东西是出去了还是进来了,就考虑这个网格随着不同的时间是如何变化的
如下划分多个网格就知道时间t为黑色的鸟,t-1应显示蓝色的鸟
物质点方法
结合了上述两个方法
- 认为这些不同的粒子都具有某些材质属性,存储在点上
- 融化的过程在网格中做
- 再将格子上的信息写回不同的粒子上去
