概念
对于一个向量,如果在线性变换中仍然留在张成的空间里,并被拉伸响应的比例,这个向量就是特征向量,每个特征向量都有一个所属的值,即特征值,特征值就是衡量特征向量在变换中拉伸或压缩比例的因子

特征向量的特征值可以为负值,表明这个向量发生了反向变换但依旧在它所张成的直线上,没发生旋转
特征向量往往用于三维下物体的旋转此时特征值必须为1,如果把特征向量认为是旋转轴来对物体进行旋转,此时只需要一个1$\times$3矩阵来表示,这要要比一个3$\times$3矩阵表示要来得直观
计算思想
特征向量符号表示
$$ \overbrace{A\vec{V}}^{矩阵向量乘积} = \overbrace{\lambda \vec{V}}^{向量数乘} $$
- A:变换矩阵
- $\vec{V}$ : 特征向量
- $\lambda$ : 特征值
初始下,该等式左右乘积的类型不同,自然难以解出$\vec{V}$和$\lambda$
等式右侧重写为某个矩阵向量乘积,即把与$\lambda$相乘改写为与一个矩阵相乘
该矩阵作用是将任一个向量乘以$\lambda$,矩阵的列表示变换后的基向量,而每个基向量都只与$\lambda$相乘,矩阵如下
$$ \begin{bmatrix} \lambda & 0 & 0 \\ 0 & \lambda & 0 \\ 0 & 0 & \lambda \end{bmatrix} = \lambda \underbrace{\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}}_{I} $$
此处的I为单位矩阵,对角元都为1,等式改写为
$$ A\vec{V} = (\lambda I)\vec{V} $$
改写后等号两侧都是矩阵向量乘法,能够将等号右侧移到左侧,提出因子V
$$ (A - \lambda I)\vec{V} = \vec{0} $$
如果$\vec{V}$本身就是零向量的话,等式自然有解,且解的目标$\vec{V}$就是零向量
$\vec{V}$为非零特征向量时,已知矩阵表示的变换将降低空间维度时,才会有一个非零向量使矩阵与它的乘积为零,即行列式为0


$$ A\vec{V} = \lambda \vec{V} \\ A\vec{V} - \lambda I \vec{V} = 0 \\ (A - \Lambda I)\vec{V} = 0 \\ det(A - \lambda I) = 0 $$

并非所有矩阵都有特征向量
例如对于旋转90度的情况矩阵$\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}$,每一个向量都发生了旋转,离开了其张成的空间
$$ det(\begin{bmatrix} -\lambda & -1 \\ 1 & -\lambda \end{bmatrix}) = (-\lambda)(-\lambda) - (-1)(1) $$
所以$\lambda = i or \lambda = -i$
无实数解表明没有特征向量
对于剪切变换,x轴上的向量就是特征值1的特征向量,于所有特征向量均属于特征值1的结论一致
属于单个特征值的特征向量也可以不在一条直线上
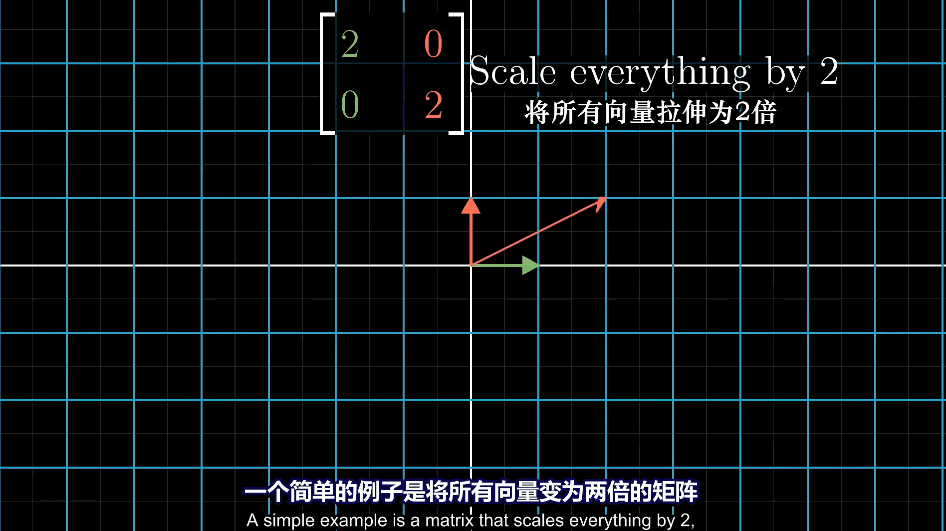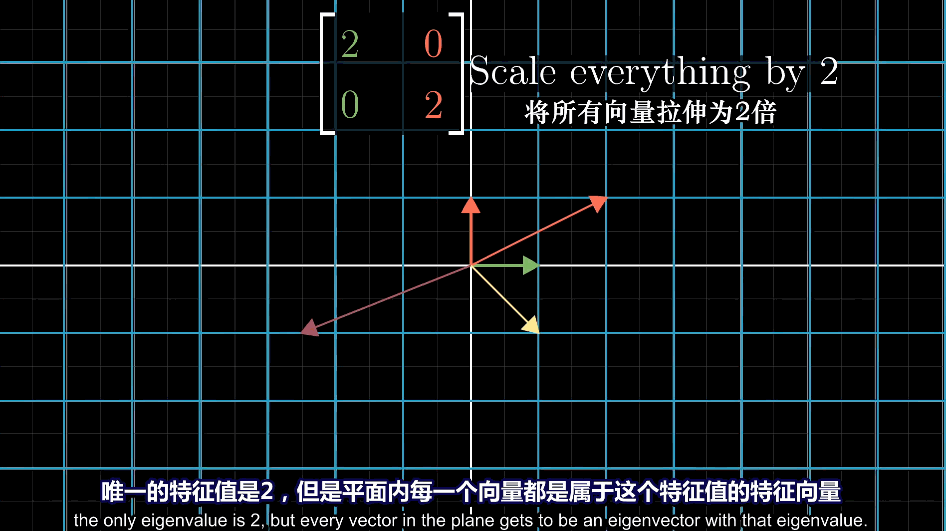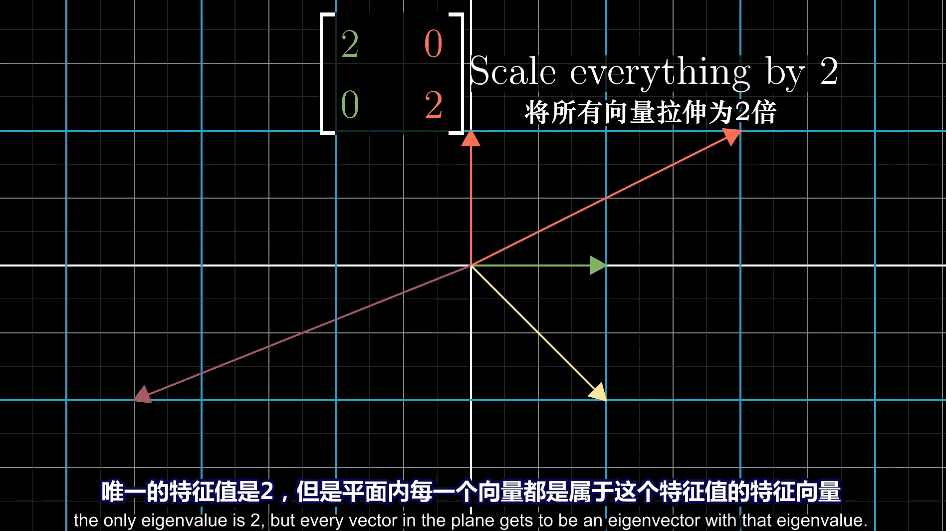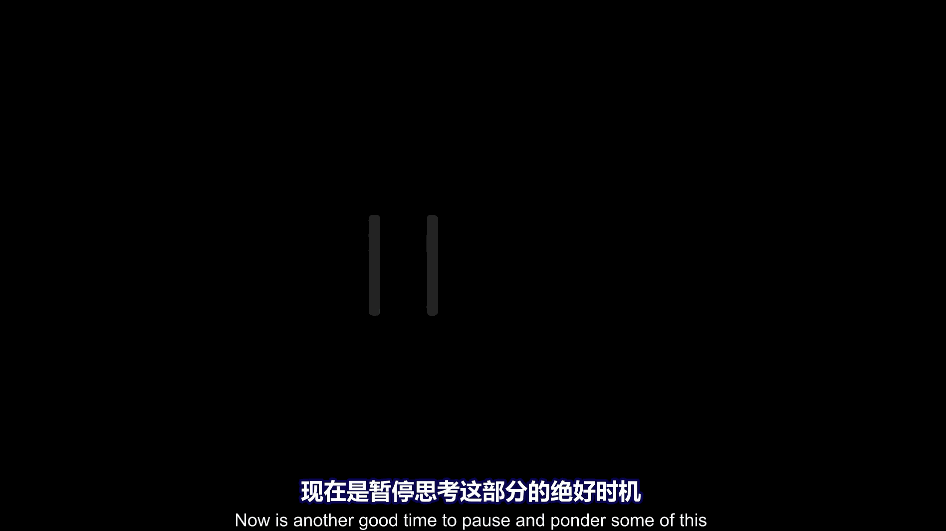
特征基
基向量恰好是特征向量时,$\hat{i}$和$\hat{j}$所属的特征值位于矩阵的对角线上,其余元素均为0
对角矩阵:除对角元以外其他元素均为0的矩阵称为对角矩阵,表示所有基向量都是特征向量,矩阵对角元就是它们所属的特征值
对角矩阵与自己多次相乘的结果往往非常容易计算,因为只需要基向量与特征值相乘

对于基向量不是特征向量的情况,如果能张成全空间的特征向量足够多到能够选出一个张成全空间的集合,就能够改变坐标系使特征向量作为基向量

一组基向量(特征向量)构成的集合称为一组特征基
给出一种便于计算矩阵多次幂的方法,即将矩阵转换到基向量是特征向量的坐标系中,然后计算多次幂再转换回标准坐标系
并非所有矩阵都能这样做,例如剪切变换就因为没有足够的特征向量构成基向量而无法转换到基向量是特征向量的坐标系中,换言之,假设能够找到一组特征基,矩阵的运算就会变得轻松许多
计算二阶矩阵特征值的技巧
传统方法
$det(\begin{bmatrix} 3 - \lambda & 1 \\ 4 & 1 - \lambda \end{bmatrix}) = (3 - \lambda) (1 - \lambda) - (1)(4) = (3-4\lambda + \lambda^2)-4 = \lambda^2-4\lambda -1$
得到矩阵的特征多项式,还需要二次方程求根得到特征值
$$ \lambda_1,\lambda_2 = \frac{4\pm\sqrt{4^2-4(1)(-1)}}{2} = \frac{4\pm\sqrt{20}}{2} = 2\pm \sqrt{5} $$
小技巧
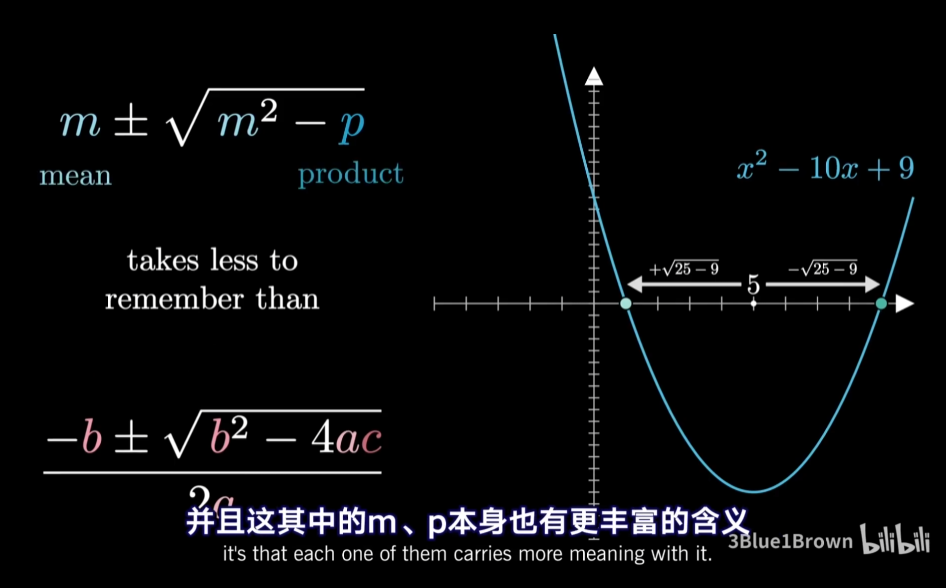
- 矩阵的迹也就是对角元的总和等于矩阵各特征值的和,即两特征值的平均数等于两个主对角元的平均数
- 二阶矩阵的行列式等于两特征值的乘积(原因:特征值描述算子在特点方向上对空间进行拉伸的程度,行列式则描述算子将面积或体积整体进行拉伸的程度)
- 如果两特征值的和为m,乘积为p,特征值则为$\lambda_1,\lambda_2 = m\pm \sqrt{m^2 - p}$

第三点的推理过程

实际计算举例
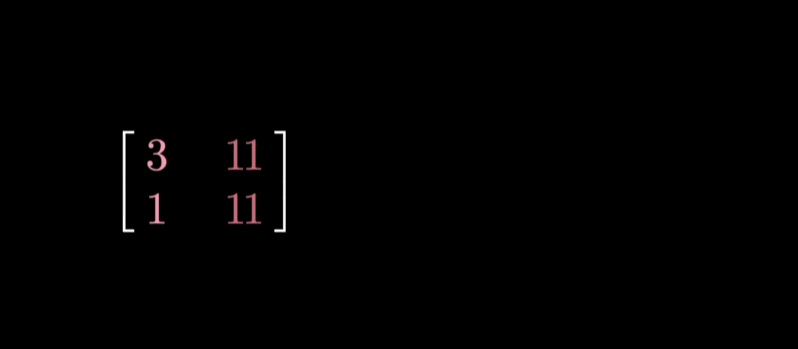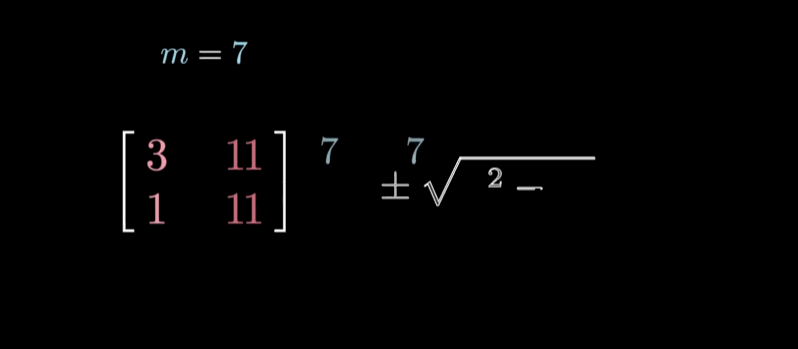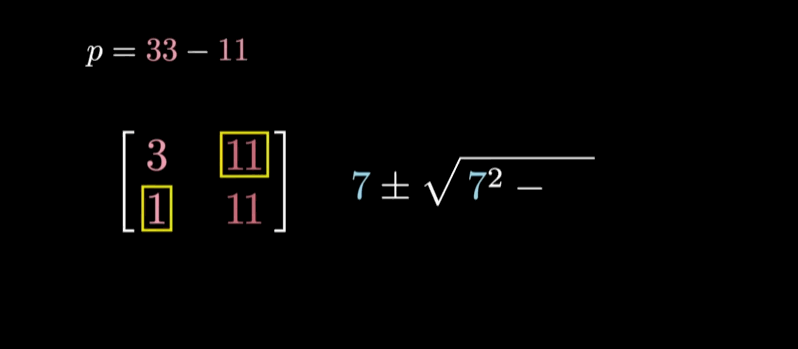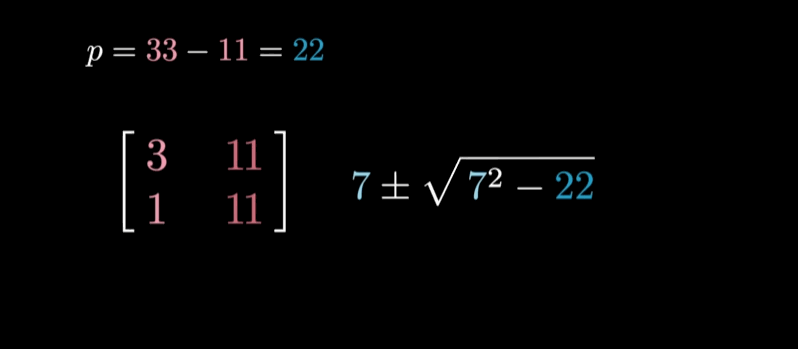
新的计算方法本质上还是解特征多项式,也是一个解二次方程的通用形式