基向量
向量空间的一组基是张成该空间的一个线性无关向量集
$\hat{i}$,指向正右方长度为1,x方向的单位向量
$\hat{j}$,指向正上方长度为1,y方向的单位向量
对于一组向量坐标,可以视为用标量相乘来缩放基向量,再将其缩放后的向量相加
$a\hat{i} + b \hat{j}$
对于$\begin{bmatrix} 3 \\ -2 \end{bmatrix}$可以认为$(3)\hat{i} + (-2)\hat{j}$
此时i与j是xy坐标系的基向量
坐标系也根据所选择的基而改变,并且对于基向量,通过不同的标量能够得到几乎所有的二维向量,并且允许在一维和二维向量间转换
线性组合
两个数乘向量的和被称为这两个向量的线性组合
$a\vec{V}+b\vec{W}$称为$\vec{V}$与$\vec{W}$的线性组合
线性体现在于当固定一个标量时,随意改动另一个标量,得到的向量终点的连续是一条连续的直线
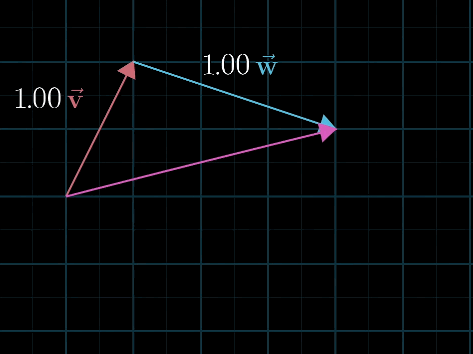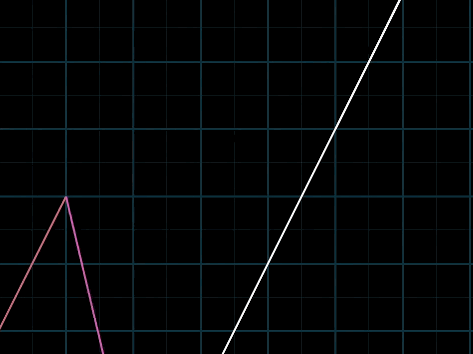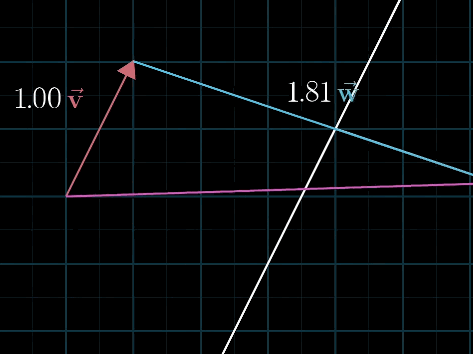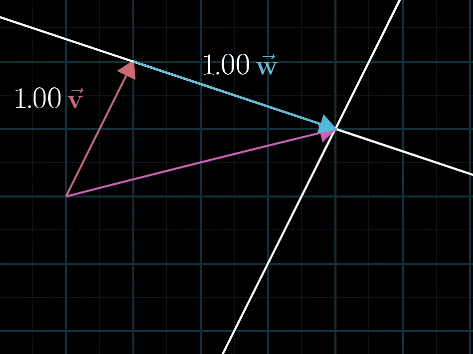
当两个向量的终点在同一直线上时,得到的向量终点都在一条直线上
张成的空间
$\vec{V}$与$\vec{W}$全部线性组合构成的向量集合称为张成的空间。对于$a\vec{V} + b\vec{W}$,a和b在实数范围内变动
当两个向量共线时,张成的空间就是终点落在一条直线上的向量的集合
本质:两个向量只通过相加和数乘能够得到的所有可能向量的集合
三维空间中,两个向量标量缩放得到的新向量集合即为三维空间中某个过原点的平面,即所有终点落在这个平面上的向量的集合就是这两个向量张成的空间
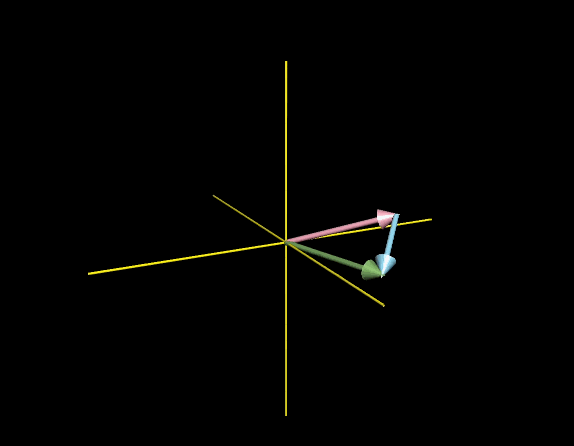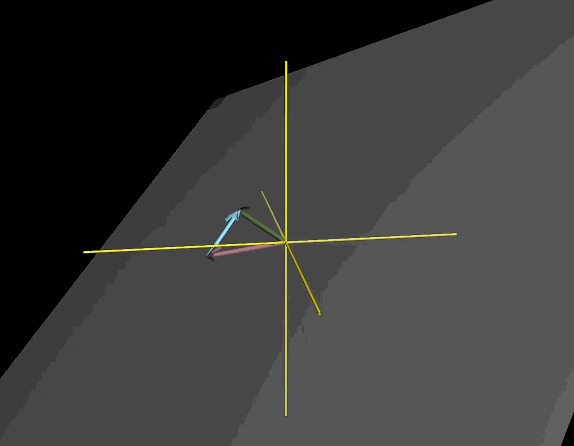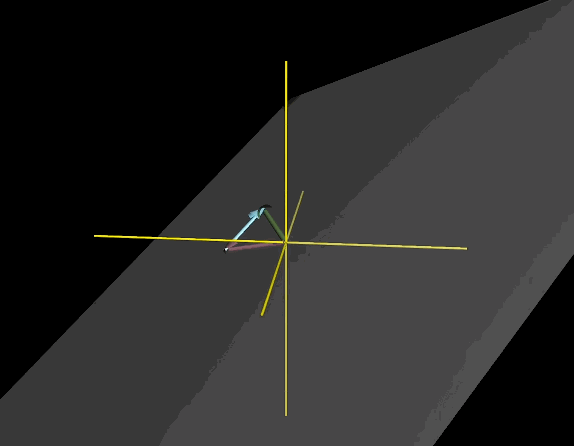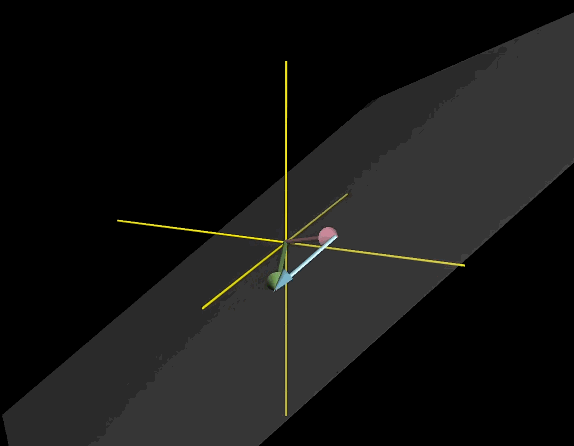
引入第三个向量后,三个向量线性组合可定义为$a\vec{V} + b\vec{W}+C\hat{u}$,对于张成空间则让a,b,c三个常数变化
第三个向量恰好落在前两个向量所张成的平面上,张成空间依旧是这个平面
第三个向量如果随机选取则几乎不可能落在前两个向量所张成的平面中,此时能够得到所有不同的三维向量
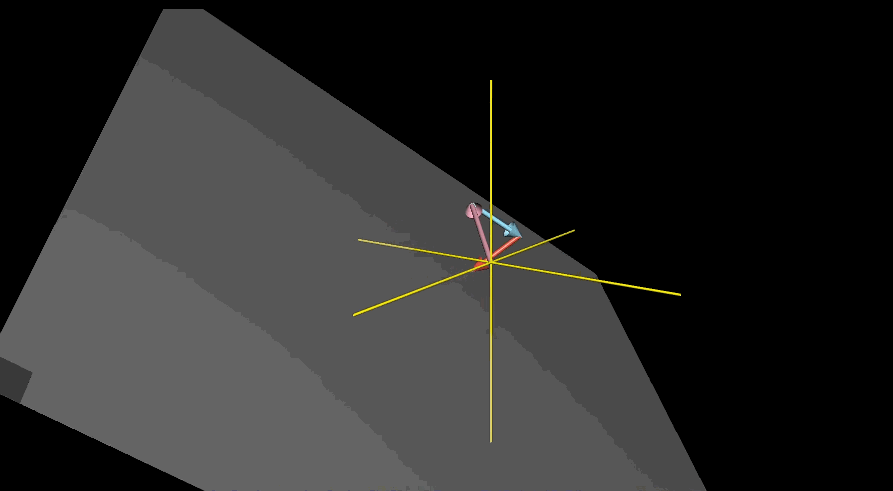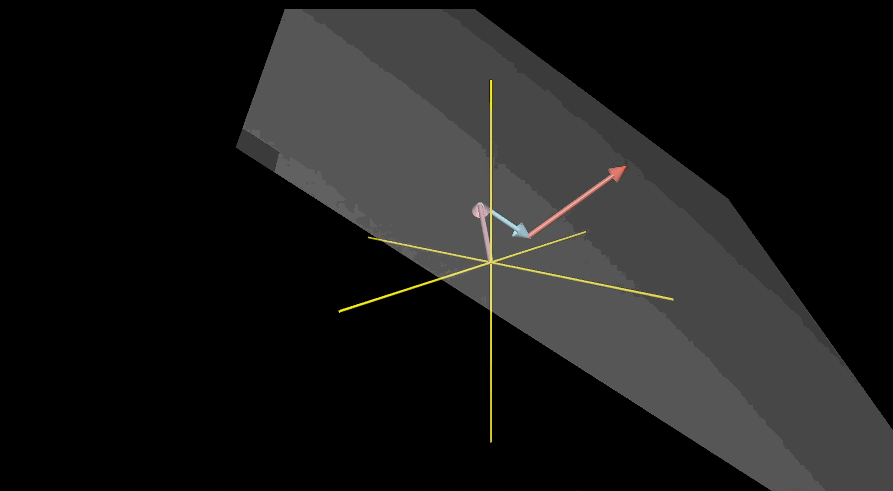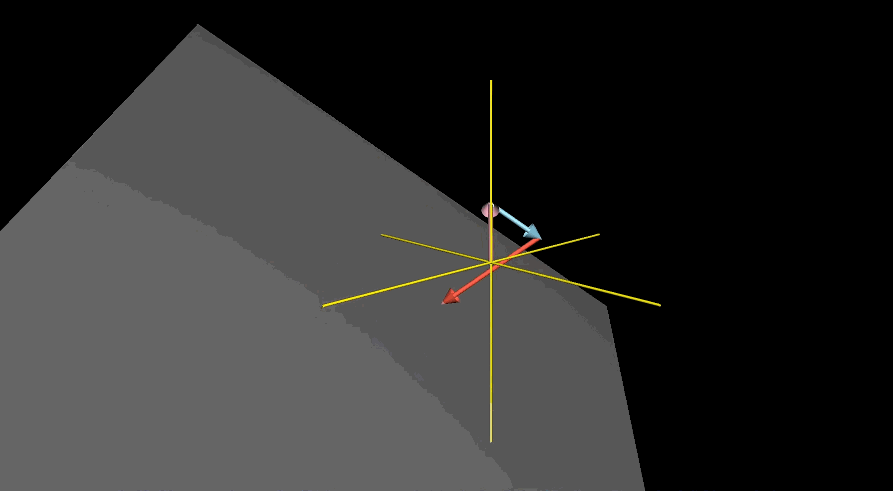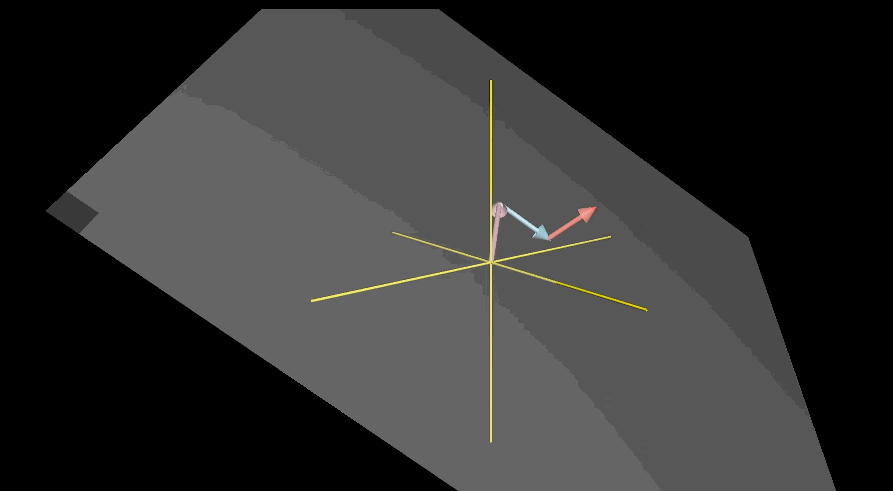
对于三维下第三个向量恰好落在前两个向量的张成平面上和二维下两个向量恰好共线的情况,可以描述为一组向量中至少有一个是多余的,没有对张成空间做出贡献,在有多个向量下,可以移出其中一个而不减小张成空间,此时往往称两个向量是线性相关的,即$\vec{u} = a\vec{V} + b \vec{W}$,也可以表述为其中一个向量可以表示为其他向量的线性组合
如果所有向量都给张成的空间增添了新的维度则称线性无关,$\vec{W} \not ={a\vec{V}},\vec{U} \not ={a\vec{V}+b\vec{W}}$
向量与点
由于在空间里的每个向量都用箭头表示时会让人感到十分拥挤,通常我们就用向量的终点来表示该向量,起点依旧位于原点
由此,同时考虑一条直线上的向量或二维向量时,只要考虑一条直线或无限大的二维平面本身即可
单向量箭头表示,多向量点表示