行列式
本质:描述线性变换过程中,一个给定区域的面积增大或减小的比例
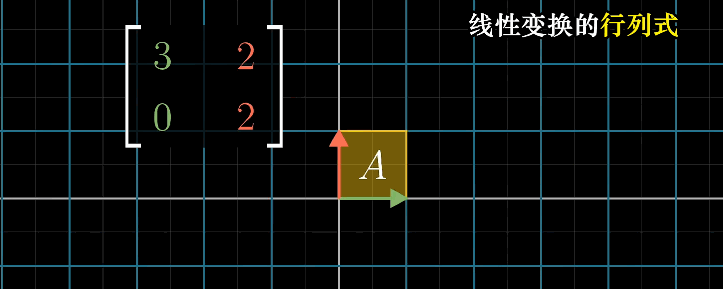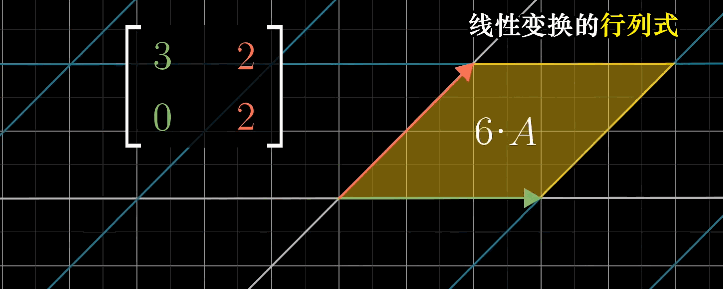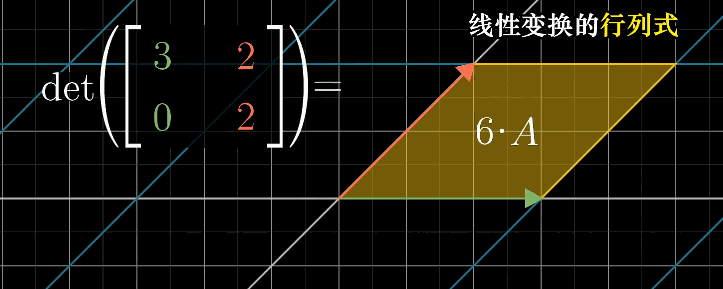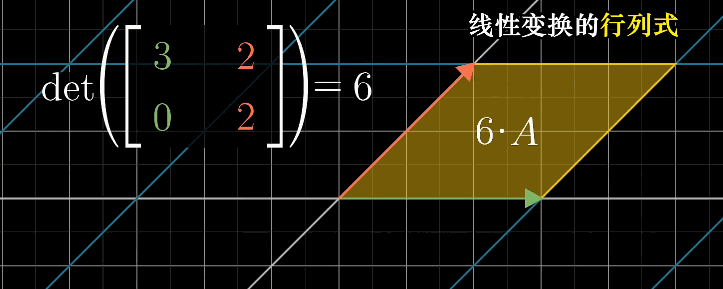
当矩阵的行列式为0时,表明将整个平面压缩到一条线甚至是一个点上,即只需要确认行列式是否为0就能了解该矩阵的变换是否导致空间降低维度
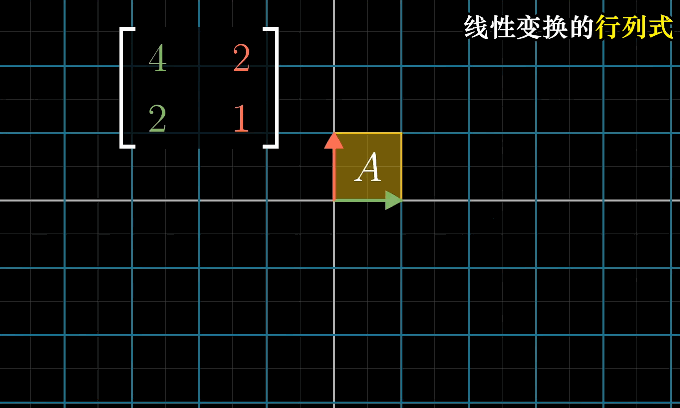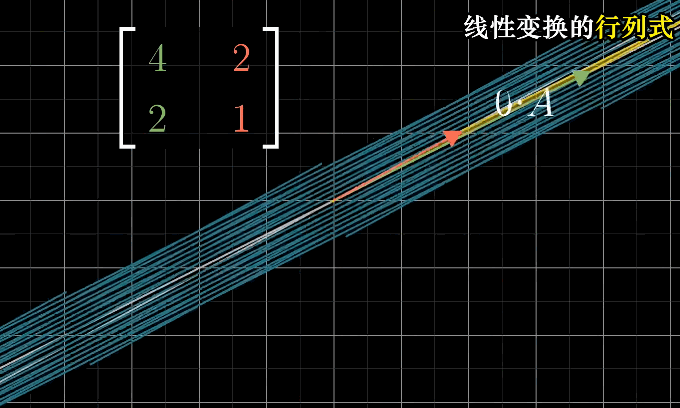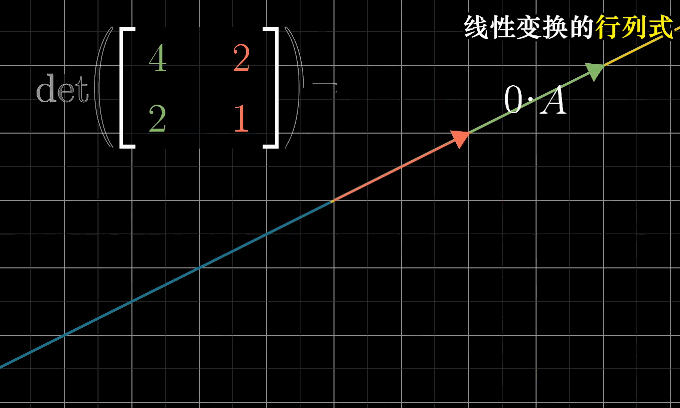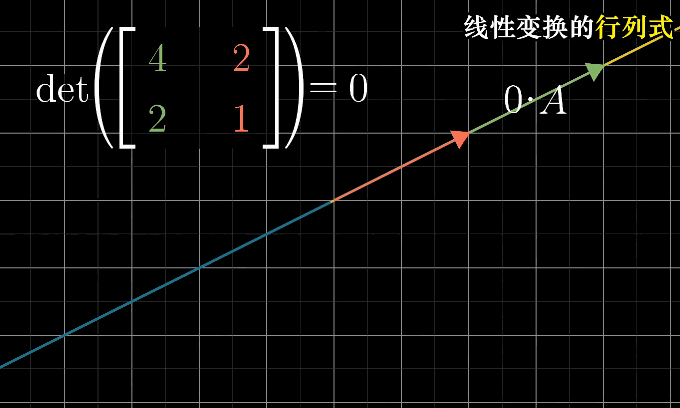
行列式中允许出现负值,负值时意味着翻转的方式来改变了空间的方向,行列式的绝对值依旧表示面积的缩放大小


三维空间行列式
与二维空间类似,此时表示体积的缩放大小
在三维空间中,往往聚焦于三个基向量围成的体积为1的立方体,在线性变换后立方体往往会变为一个平行六面体,此时行列式可以简单看作这个平行六面体的体积

行列式为0时,意味着立方体的体积变换为0,即一个平面或一条直线,甚至一个点
行列式为负值时,涉及空间方向改变
空间正向使用右手法则来定义即右手食指指向$\hat{i}$方向,中指指向$\hat{j}$方向,大拇指指向$\hat{k}$方向,如果在变换后只能用左手表示,则说明行列式为负

行列式计算公式
$$ det(\begin{bmatrix} a & b \\ c & d \end{bmatrix}) = ad -bc $$
直观理解:
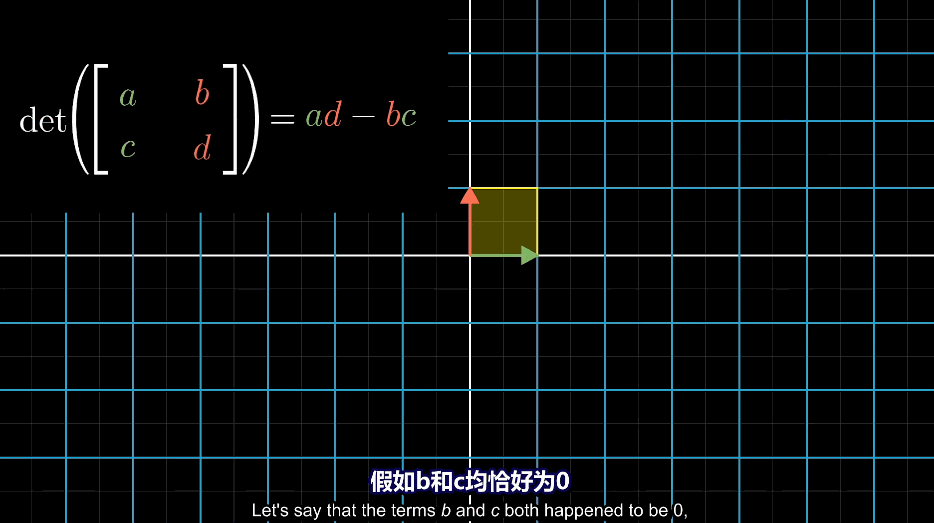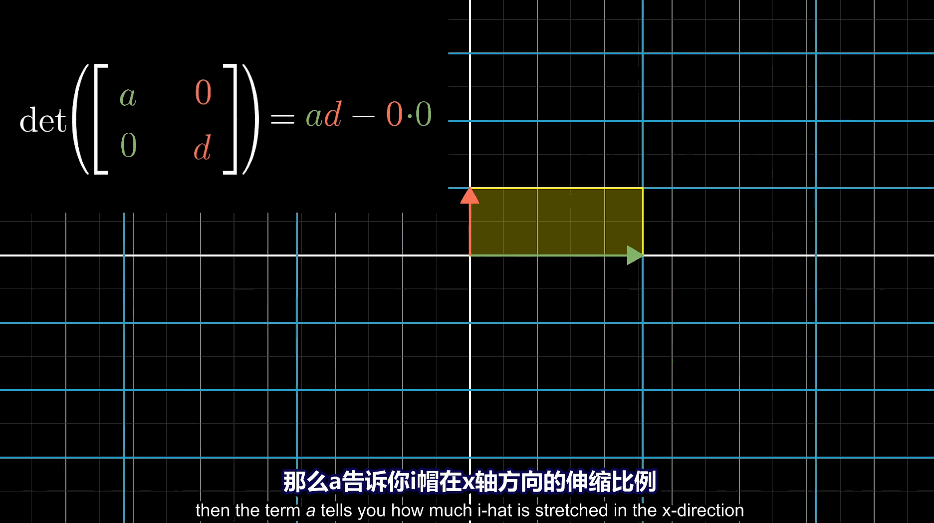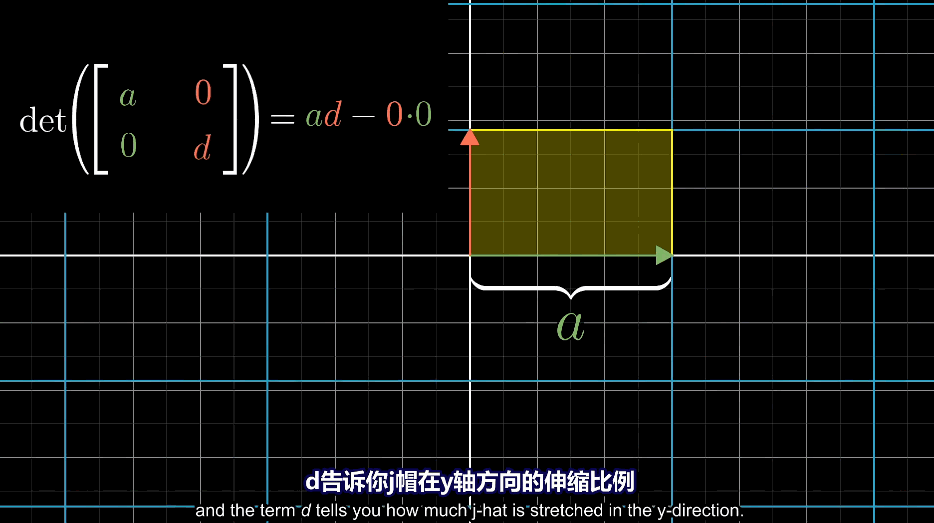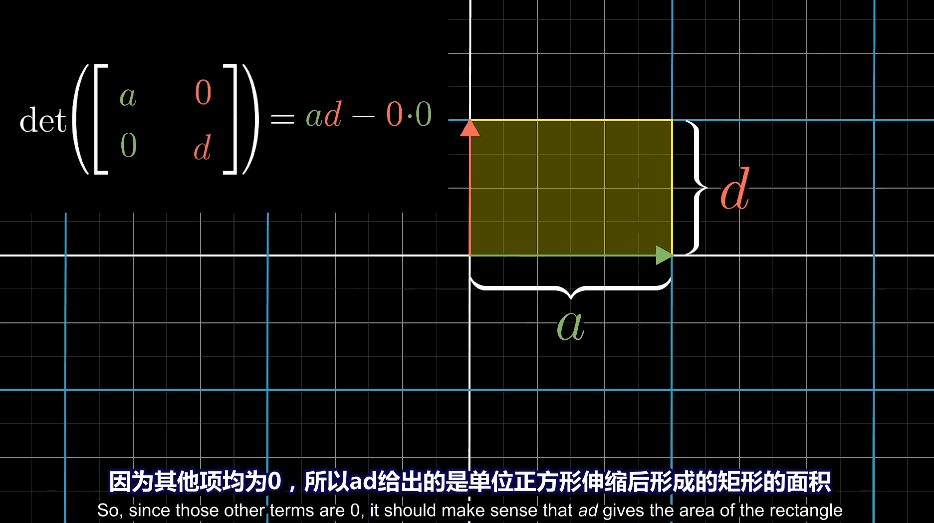
即使其中一项为0,最后得到的依旧是一个平行四边形

公式中bc值的确切含义
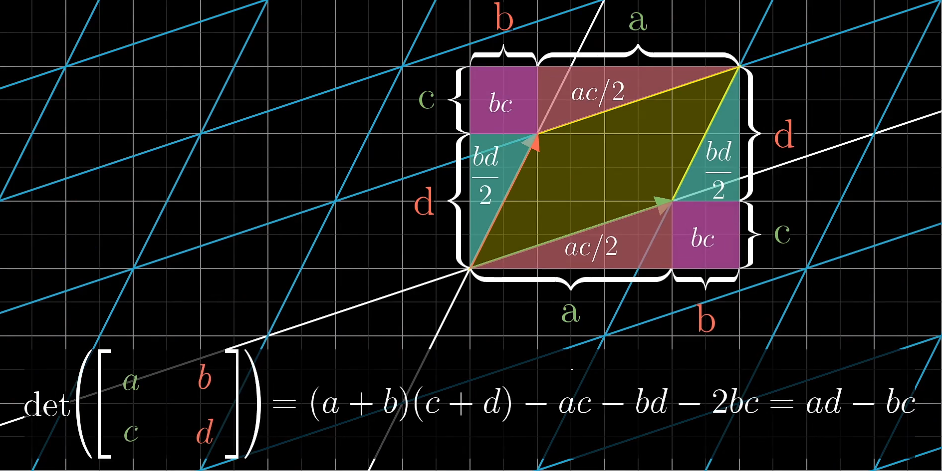
三维空间中的行列式计算
$det(\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}) = a \ det(\begin{bmatrix} e & i \\ h & f \end{bmatrix}) - b \ det(\begin{bmatrix} d & f \\ g & i \end{bmatrix}) + c \ det(\begin{bmatrix} d & e \\ g & h \end{bmatrix}) $
矩阵相乘本质是两次线性变换,而行列式是线性变换后面积变化比例,在顺序不变情况下,自然行列式的值乘积相等
$det(M_1M_2) = det(M_1) det(M_2)$