本文的论述中将向量写作矩阵的列,与教科书中将向量写作矩阵的行不同,由于转置不改变行列式的值,在本文中出于直观考虑按列处理向量不会改变结果
叉乘的标准描述
已知两个向量$\vec{V}$和$\vec{W}$,考虑它们所张成的平行四边形,此时$\vec{V}$和$\vec{W}$的叉乘($\vec{V}\times\vec{W}$)就是这个平行四边形的面积
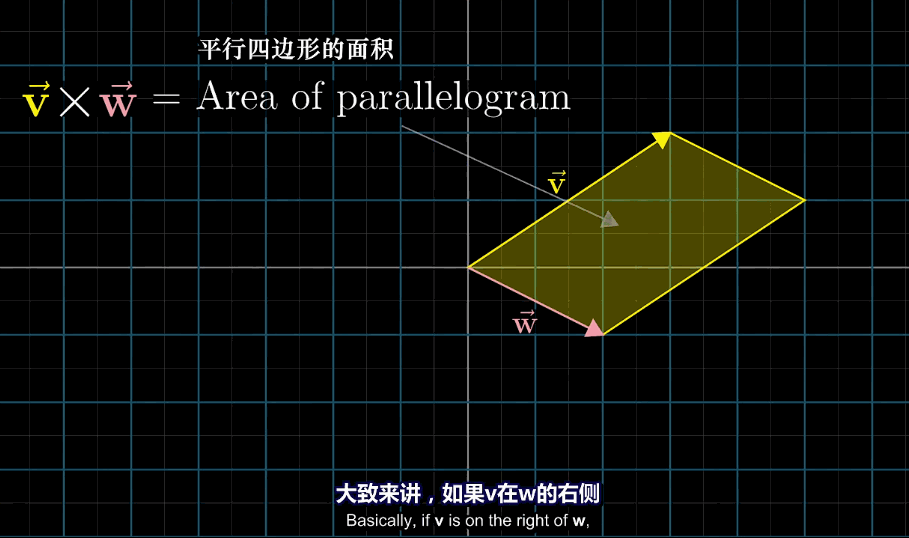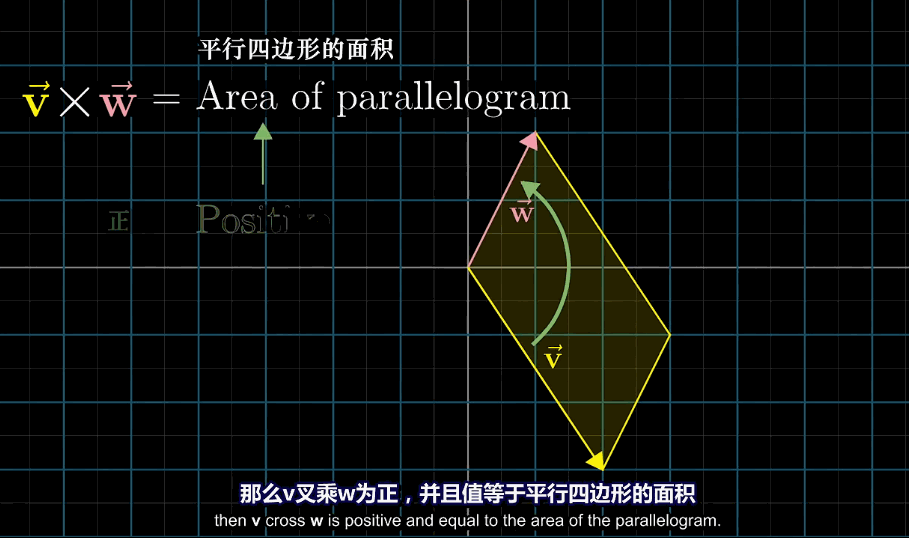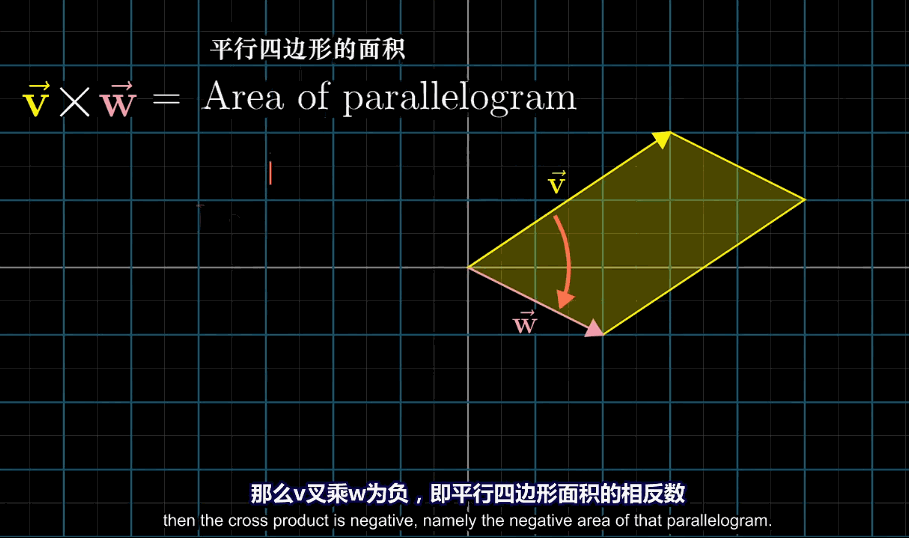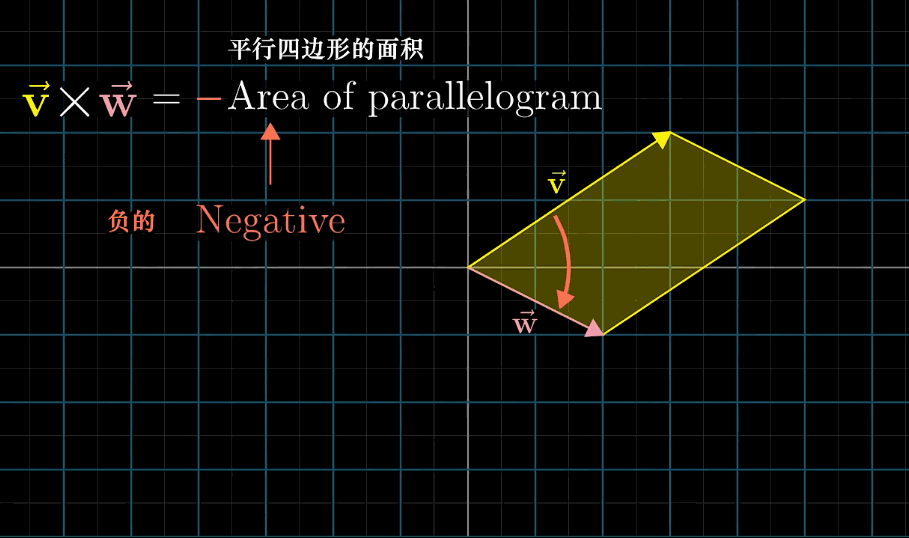
叉乘是顺序强相关的计算,计算顺序与方向或叉乘值的正负相关,顺序交换后通常叉乘的值相反
记忆顺序的方法
将按序求两个基向量的叉乘($\hat{i}\times\hat{j}$)记为正的,实质上叉乘的正方向定义就是基向量叉乘的方向
如下图中,由于$\vec{V}$在$\vec{W}$的左侧,与基向量相反,所以叉乘的值就是负的
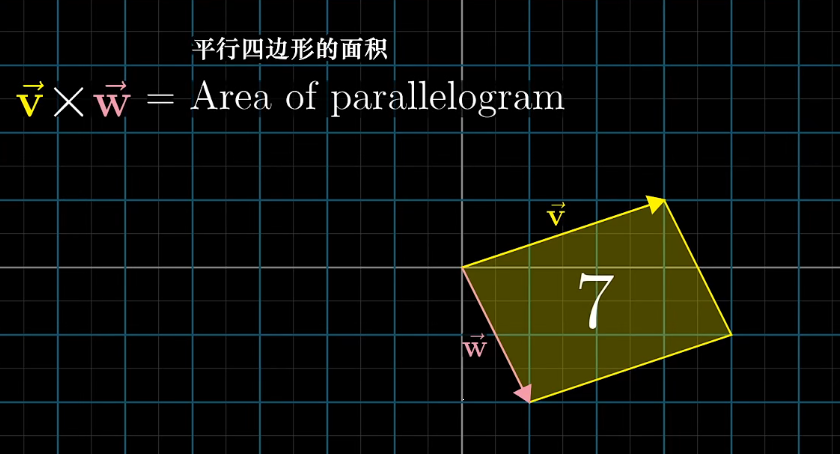
叉乘的计算
如果看过之前有关行列式的文章就能注意到
行列式与叉乘在几何的表示有些类似
- 叉乘
- 两个向量所张成的平面
- 行列式
- 两个向量在线性变换后构成的平行四边形与基向量构成的正方形的面积比例
二维向量
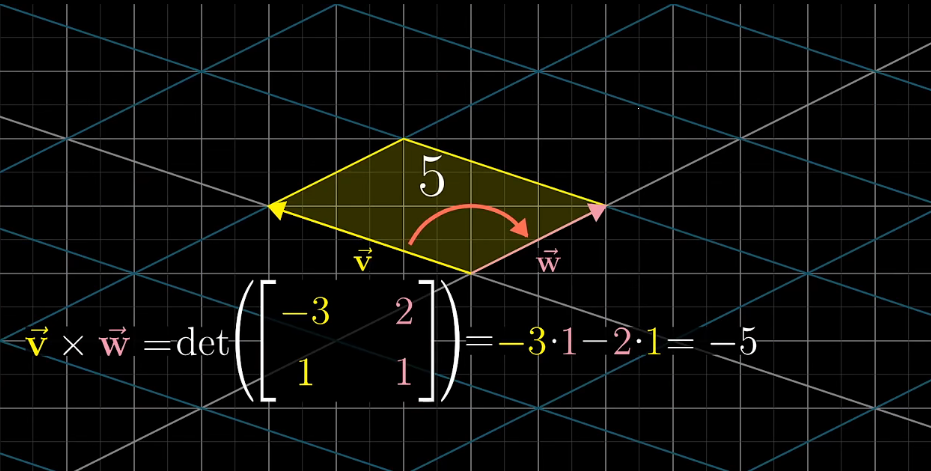
$$ \vec{V}\times\vec{W} = \begin{bmatrix} -3 \\ 1 \end{bmatrix} \times \begin{bmatrix} 2 \\ 1 \end{bmatrix} = det(\begin{bmatrix} -3 & 2 \\ 1 & 1 \end{bmatrix}) = -3 \cdot 1 - 2 \cdot 1 = -5 $$
即将第一个乘数作为第一列,第二个乘数作为第二列构成一个矩阵然后计算这个矩阵的行列式
本质是构成的矩阵记录了将基向量$\hat{i}$和$\hat{j}$移至$\vec{V}$和$\vec{W}$的线性变换,行列式便度量了变换前后的面积变换比例,即此时的行列式的值就是平行四边形的面积就是叉乘的值,当然变换后的$\vec{V}$在$\vec{W}$的左侧,叉乘的值为负值
当两个向量垂直或是越趋近于垂直时,平行四边形的面积越大,叉乘的值越大,越趋近于同向,平行四边形越小,叉乘值越小

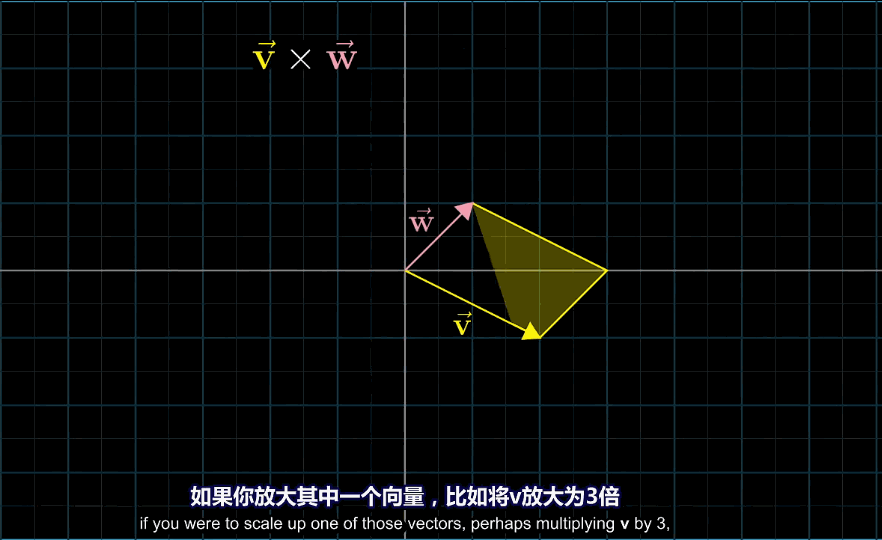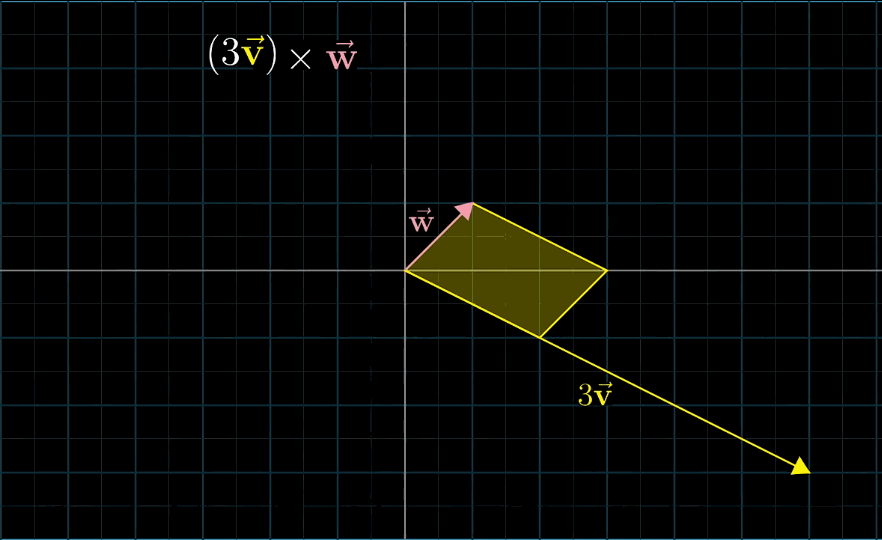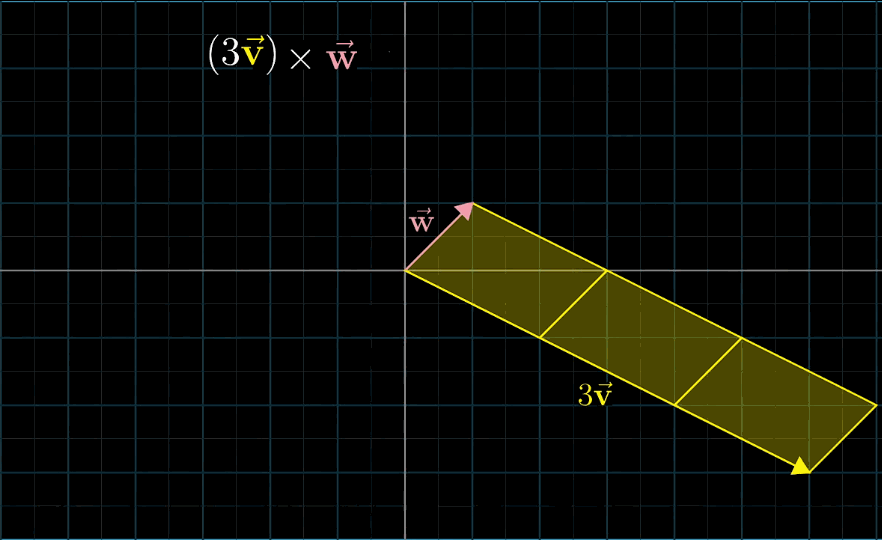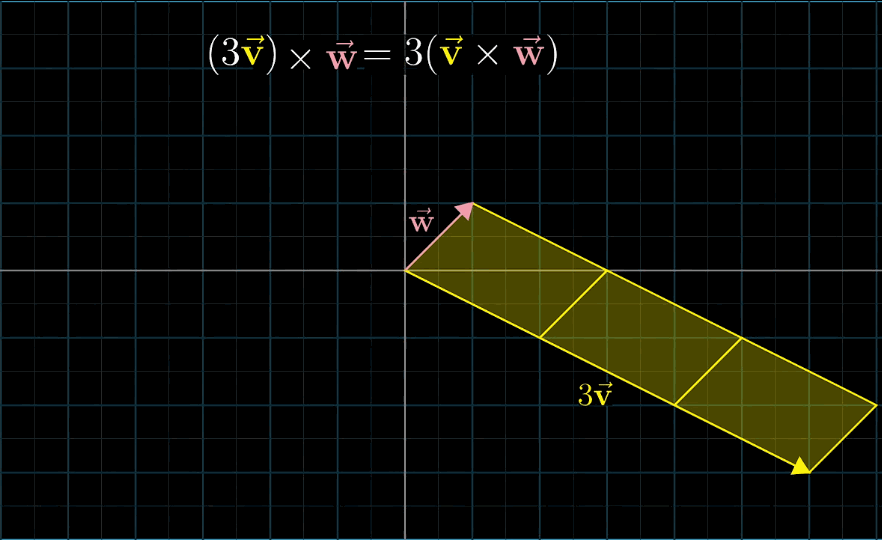
三维向量
叉乘:两个三维向量生成第三个三维向量垂直于前两个三维向量所构成的面
方向则由右手定则定义
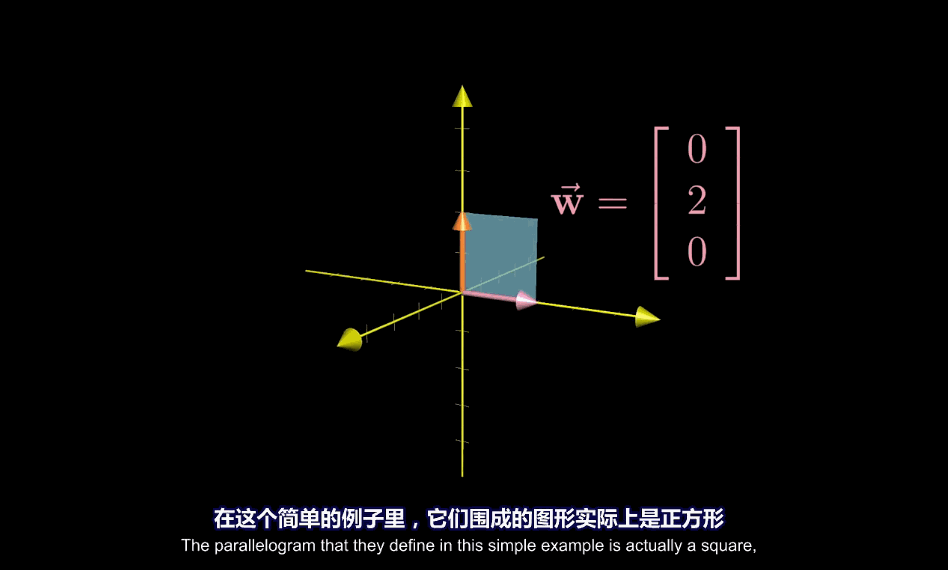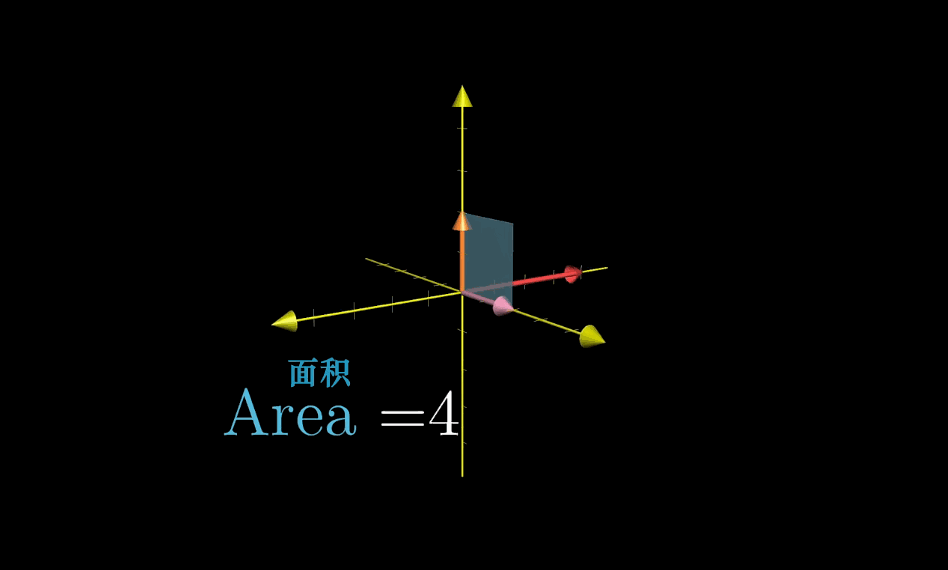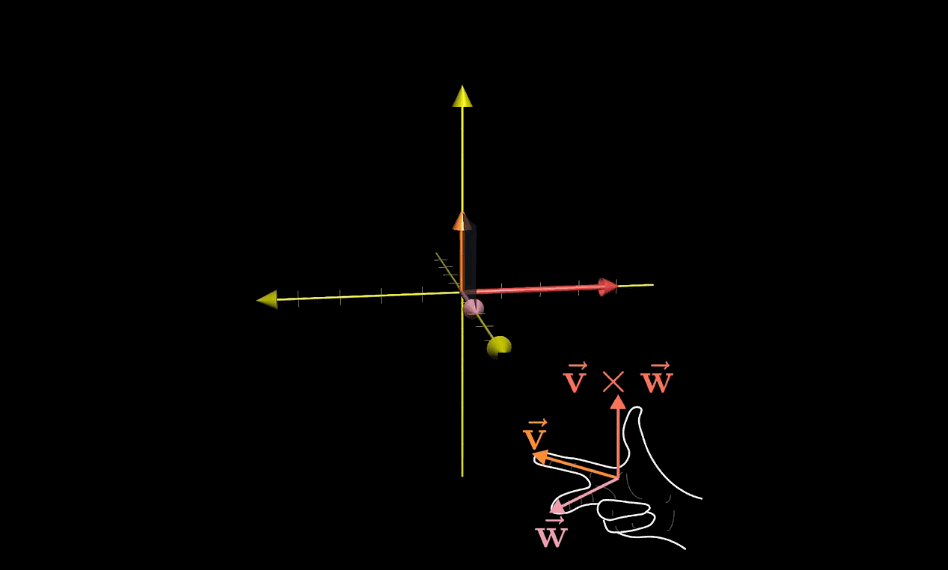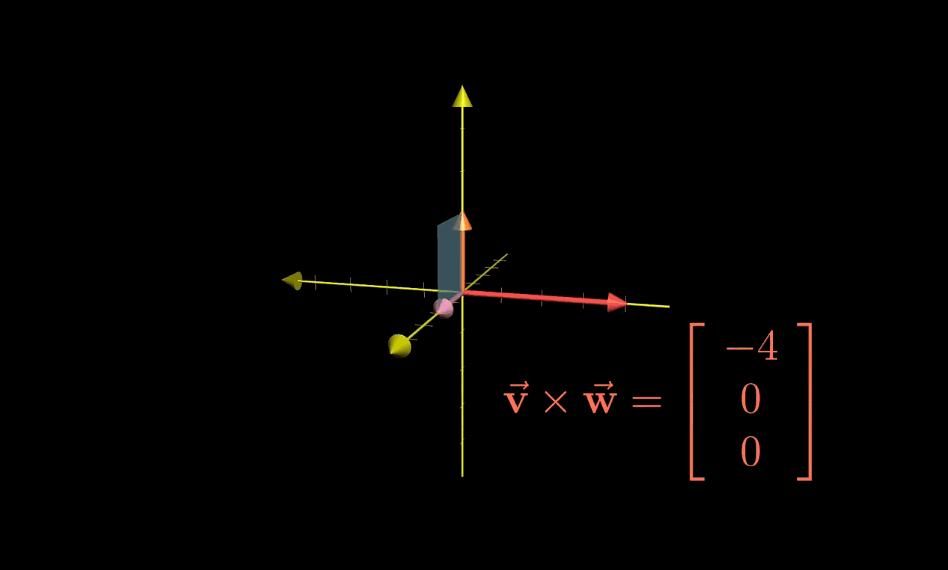
计算公式
$$ \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix} \times \begin{bmatrix} w_1 \\ w_2 \\ w_3 \end{bmatrix} = \begin{bmatrix} v_2 \cdot w_3 - w_2 \cdot v_3 \\ v_3 \cdot w_1 - w_3 \cdot v_1 \\ v_1 \cdot w_2 - w_1 \cdot v2 \end{bmatrix} $$
为了便于记忆,可以使用以下三阶行列式来计算
$$ \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix} \times \begin{bmatrix} w_1 \\ w_2 \\ w_3 \end{bmatrix} = det( \begin{bmatrix} \hat{i} & v_1 & w_1 \\ \hat{j} & v_2 & w_2 \\ \hat{k} & v_3 & w_3 \end{bmatrix}) = \hat{i}(v_2w_3 - v_3w_2)+\hat{j}(v_3w_1 - v_1w_3) + \hat{k}(v_1w_2 - v_2w_1) $$
此时第一列是三维空间的基向量作为矩阵元,在符号上只需要认为括号中的线性组合所决定的向量是唯一与$\vec{V}$和$\vec{W}$垂直长度为$\vec{V}$和$\vec{W}$围成的平行四边形的面积且遵循右手定则的向量
由上述公式我们能推导一个线性函数,
$$ f(\begin{bmatrix} x \\ y \\ z \end{bmatrix}) = det( \begin{bmatrix} x & v_1 & w_1 \\ y & v_2 & w_2 \\ z & v_3 & w_3 \end{bmatrix}) $$
由于该函数是线性的,意味着可以用矩阵乘法来描述,可以用一个1$\times$3矩阵来表示这个变换
而对于多维空间到一维空间的变换,可以进行转置,将横着的矩阵竖起来,变成如下样子,将变换视为与这个特定向量的点积而不影响结果
$$ \overbrace{\begin{bmatrix} P_1 \\ P_2 \\ P_3 \end{bmatrix}}\vec{P} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = det( \begin{bmatrix} x & v_1 & w_1 \\ y & v_2 & w_2 \\ z & v_3 & w_3 \end{bmatrix}) $$
此时问题演变为,寻找向量P,使得其与任一向量的点积等于一个第一列为该向量的3$\times$3矩阵的行列式,其余则分别为V和W的坐标
计算意义
上式能进一步整理为为
$P_1\cdot X + P_2 \cdot Y + P_3 \cdot Z =\\ X(v_2w_3 - v_3w_2) +\\ Y(v_3w_1 - v_1w_3) +\\ Z(v_1w_2 - v_2w_1)$
由于常数涉及V和W坐标的特点组合,可以进一步认为这些就是P的坐标
$$ P_1 = v_2w_3 - v_3w_2 \\ P_2 = v_3w_1 - v_1w_3 \\ P_3 = v_1w_2 - v_2w_1 $$
这些计算流程与前面将基向量放进矩阵第一列计算然后合并各项系数没有区别,插入基向量只是为了提醒我们应将系数认为是一个向量的坐标
$$ \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix} \times \begin{bmatrix} w_1 \\ w_2 \\ w_3 \end{bmatrix} = det( \begin{bmatrix} \hat{i} & v_1 & w_1 \\ \hat{j} & v_2 & w_2 \\ \hat{k} & v_3 & w_3 \end{bmatrix}) = \hat{i}(v_2w_3 - v_3w_2)+\hat{j}(v_3w_1 - v_1w_3) + \hat{k}(v_1w_2 - v_2w_1) $$
上述方法的几何解释
